Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in Figure, a bullet with mass $m = 50$ g is fired into a wooden block of mass $M=500$ g. The block is attached to a spring with spring constant $k=1000$ N/m. The bullet embeds itself in the block, and the combination compresses the spring by a maximum distance of $x=50$ cm. The horizontal surface is frictionless.
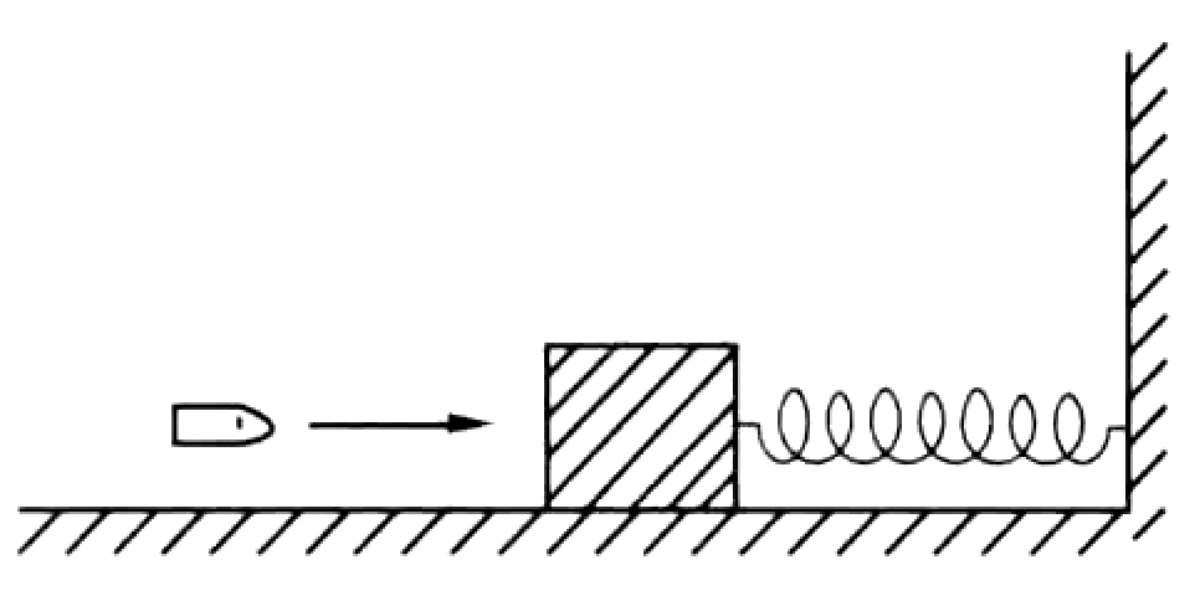
P0585-problem-1
This is a two-step process. First, a perfectly inelastic collision between the bullet and the block, where momentum is conserved. Second, the compression of the spring by the block-bullet system, where mechanical energy is conserved. Let $v$ be the initial bullet speed and $V$ be the speed of the block-bullet system just after impact. Momentum conservation (collision):
$$mv = (m+M)V$$Energy conservation (spring compression):
$$\frac{1}{2}(m+M)V^2 = \frac{1}{2}kx^2$$From the energy equation, solve for $V$: $V = x\sqrt{\frac{k}{m+M}}$. Substitute $V$ into the momentum equation and solve for $v$:
$$v = \frac{m+M}{m}V = \frac{m+M}{m} x \sqrt{\frac{k}{m+M}} = \frac{x}{m}\sqrt{k(m+M)}$$