Source: Principles of Physics
Problem Sets:
Problem
A block of mass $m$ has an initial speed $v_A$ on a horizontal, frictionless surface. It moves up a frictionless curved ramp to a height $h$, where it encounters a rough section of length $L$ on an incline of angle $\theta$. The coefficient of kinetic friction on this section is $\mu_k$. Point B marks the end of the rough section.
- If the block reaches point B, what is its speed $v_B$?
- If the block does not reach point B, what is its greatest height $H_{max}$ above the initial surface?
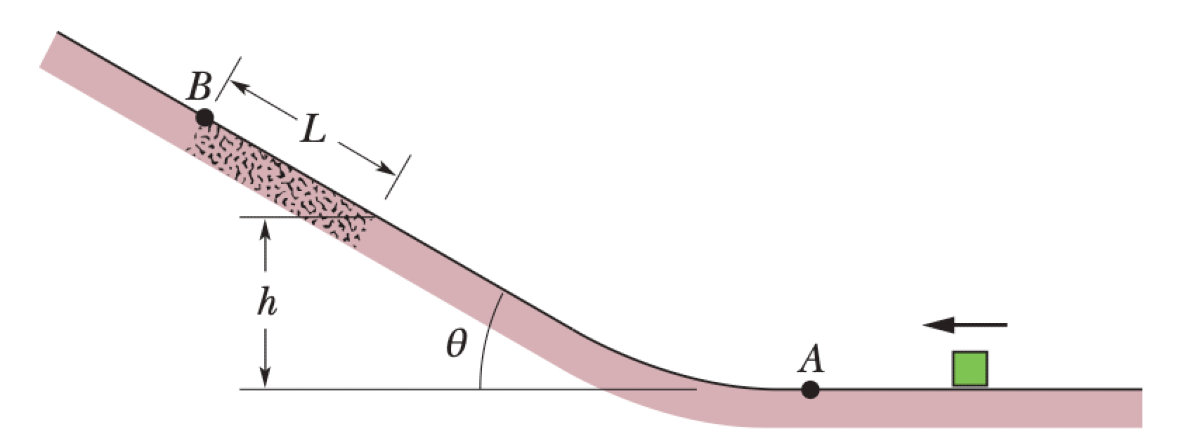
P0561-problem-1
The block reaches point B if $v_A^2 \ge 2g(h + L(\sin\theta + \mu_k\cos\theta))$. [Q1] If it reaches B, its speed is $v_B = \sqrt{v_A^2 - 2g(h + L(\sin\theta + \mu_k\cos\theta))}$. [Q2] If it does not reach B, its maximum height is $H_{max} = h + \frac{(v_A^2 - 2gh)\sin\theta}{2g(\sin\theta + \mu_k\cos\theta)}$.
We apply the work-energy theorem, where the change in mechanical energy equals the work done by the non-conservative force of friction: $\Delta E_{mech} = W_{f}$. Let the initial level at point A be the reference for potential energy ($y_A=0$).
The work done by friction over a distance $s$ on the incline is $W_f = -f_k s = -(\mu_k N) s$. The normal force is $N = mg\cos\theta$, so $W_f = -\mu_k mgs\cos\theta$.
The change in mechanical energy from A to a final point F is $\Delta E_{mech} = (\frac{1}{2}mv_F^2 + mgy_F) - \frac{1}{2}mv_A^2$. Combining these gives:
$$(\frac{1}{2}mv_F^2 + mgy_F) - \frac{1}{2}mv_A^2 = -\mu_k mgs\cos\theta$$First, we determine if the block reaches point B. This occurs if the final kinetic energy at B is non-negative. At point B, the final height is $y_F = y_B = h + L\sin\theta$ and the distance of friction is $s=L$.
$$\frac{1}{2}mv_B^2 + mg(h + L\sin\theta) - \frac{1}{2}mv_A^2 = -\mu_k mgL\cos\theta$$ $$v_B^2 = v_A^2 - 2g(h + L\sin\theta) - 2g\mu_k L\cos\theta = v_A^2 - 2g(h + L(\sin\theta + \mu_k\cos\theta))$$The block reaches B if $v_B^2 \ge 0$.
[Q1] If the block reaches B, its speed is found from the expression for $v_B^2$:
$$v_B = \sqrt{v_A^2 - 2g(h + L(\sin\theta + \mu_k\cos\theta))}$$[Q2] If the block does not reach B ($v_B^2 < 0$), it stops momentarily at a distance $d < L$ along the rough section. At this point, the final speed is $v_F=0$. The maximum height is $H_{max} = h + d\sin\theta$, and the friction distance is $s=d$. The work-energy equation becomes:
$$(0 + mg(h + d\sin\theta)) - \frac{1}{2}mv_A^2 = -\mu_k mgd\cos\theta$$Solving for $d$:
$$mgd(\sin\theta + \mu_k\cos\theta) = \frac{1}{2}mv_A^2 - mgh$$ $$d = \frac{v_A^2 - 2gh}{2g(\sin\theta + \mu_k\cos\theta)}$$The maximum height is then:
$$H_{max} = h + d\sin\theta = h + \frac{(v_A^2 - 2gh)\sin\theta}{2g(\sin\theta + \mu_k\cos\theta)}$$