Source: Principles of Physics
Problem
A block of mass $m$ slides along a track with an initial speed $v_0$. The track is frictionless until the block reaches a higher level, at a height $h$ above the starting point. On this higher level, the coefficient of kinetic friction is $\mu_k$. The block slides a distance $d$ on this frictional surface before coming to rest.
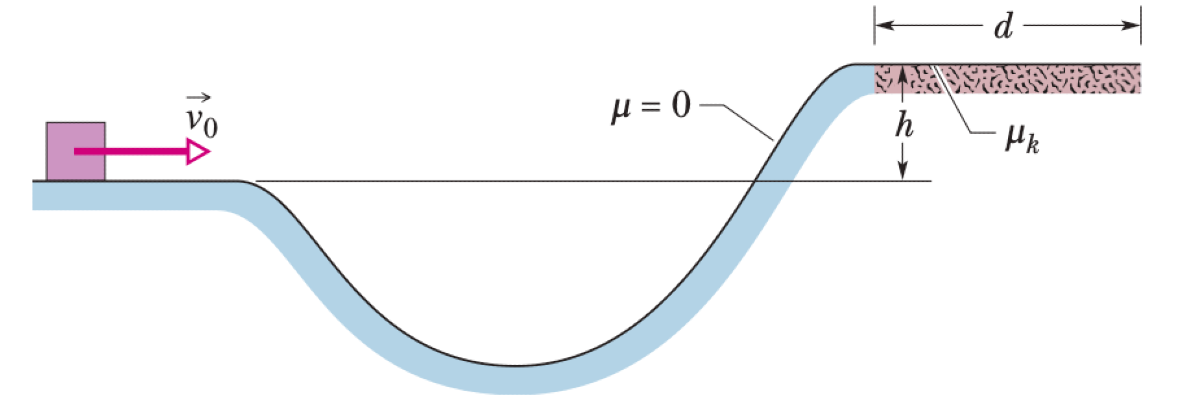
P0554-problem-1
We apply the work-energy theorem, where the change in the total mechanical energy of the block is equal to the work done by the non-conservative force of friction.
$$\Delta E_{mech} = W_{friction}$$The change in mechanical energy is the sum of the changes in kinetic and potential energy, $\Delta E_{mech} = (K_f - K_i) + (U_f - U_i)$. Let the initial state be the reference level for potential energy ($U_i = 0$). The initial kinetic energy is $K_i = \frac{1}{2}mv_0^2$. The block comes to rest ($K_f = 0$) at a height $h$ ($U_f = mgh$).
The work done by friction is $W_{friction} = -f_k d = -\mu_k N d$. On the final horizontal surface, the normal force is $N = mg$, so $W_{friction} = -\mu_k mg d$.
Substituting these into the work-energy equation:
$$(0 - \frac{1}{2}mv_0^2) + (mgh - 0) = -\mu_k mg d$$ $$mgh - \frac{1}{2}mv_0^2 = -\mu_k mg d$$The mass $m$ cancels. We can solve for the distance $d$:
$$\mu_k g d = \frac{1}{2}v_0^2 - gh$$ $$d = \frac{\frac{1}{2}v_0^2 - gh}{\mu_k g} = \frac{v_0^2 - 2gh}{2\mu_k g}$$