Source: Principles of Physics
Problem
A ball of mass $m$ is attached to a string of length $L$. The other end of the string is fixed. The ball is released from rest with the string held in a horizontal position. A fixed peg is located at point $P$, a vertical distance $d$ below the fixed end. When the ball swings down, the string catches on the peg, and the ball continues its swing about the peg.
- What is the speed of the ball when it reaches its lowest point?
- What is its speed when it reaches its highest point after the string catches on the peg?
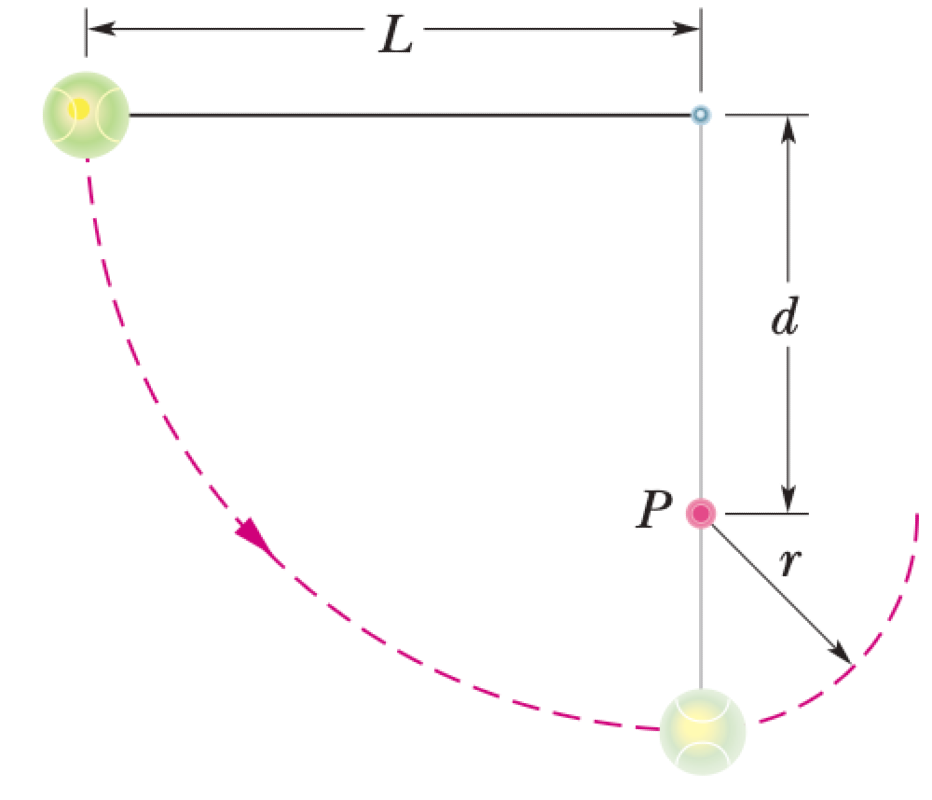
P0552-problem-1
[A1] $v_{low} = \sqrt{2gL}$ [A2] $v_{high} = \sqrt{2g(2d - L)}$
The mechanical energy of the ball is conserved because the tension force is always perpendicular to the velocity, and gravity is a conservative force. Let the potential energy be zero ($U=0$) at the lowest point of the swing.
The initial energy $E_i$ when the ball is released from the horizontal position (height $L$ above the lowest point) is purely potential:
$$E_i = K_i + U_i = 0 + mgL = mgL$$[A1] At the lowest point, the height is zero, and the energy $E_{low}$ is purely kinetic. Let the speed be $v_{low}$.
$$E_{low} = K_{low} + U_{low} = \frac{1}{2}mv_{low}^2 + 0$$By conservation of energy, $E_i = E_{low}$:
$$mgL = \frac{1}{2}mv_{low}^2$$ $$v_{low} = \sqrt{2gL}$$[A2] After the string hits the peg, the ball swings around the peg in a circle of radius $r = L-d$. The speed at the lowest point remains $v_{low}$. The highest point of this new swing is a vertical distance of $2r$ above the lowest point. Let the speed at this highest point be $v_{high}$. The energy $E_{high}$ at this point is:
$$E_{high} = K_{high} + U_{high} = \frac{1}{2}mv_{high}^2 + mg(2r)$$ $$E_{high} = \frac{1}{2}mv_{high}^2 + 2mg(L-d)$$By conservation of energy, $E_{low} = E_{high}$:
$$\frac{1}{2}mv_{low}^2 = \frac{1}{2}mv_{high}^2 + 2mg(L-d)$$Substituting $v_{low}^2 = 2gL$:
$$mgL = \frac{1}{2}mv_{high}^2 + 2mg(L-d)$$ $$\frac{1}{2}v_{high}^2 = gL - 2g(L-d) = gL - 2gL + 2gd = g(2d-L)$$ $$v_{high} = \sqrt{2g(2d - L)}$$This requires $2d \ge L$ for the ball to reach the top.