Source: Principles of Physics
Problem Sets:
Problem
A block slides a distance $d$ down a frictionless ramp inclined at an angle $\theta$. A rope pulls on the block with a constant force of magnitude $F_r$ directed up the ramp. During this displacement, the block's kinetic energy increases by $\Delta K$.
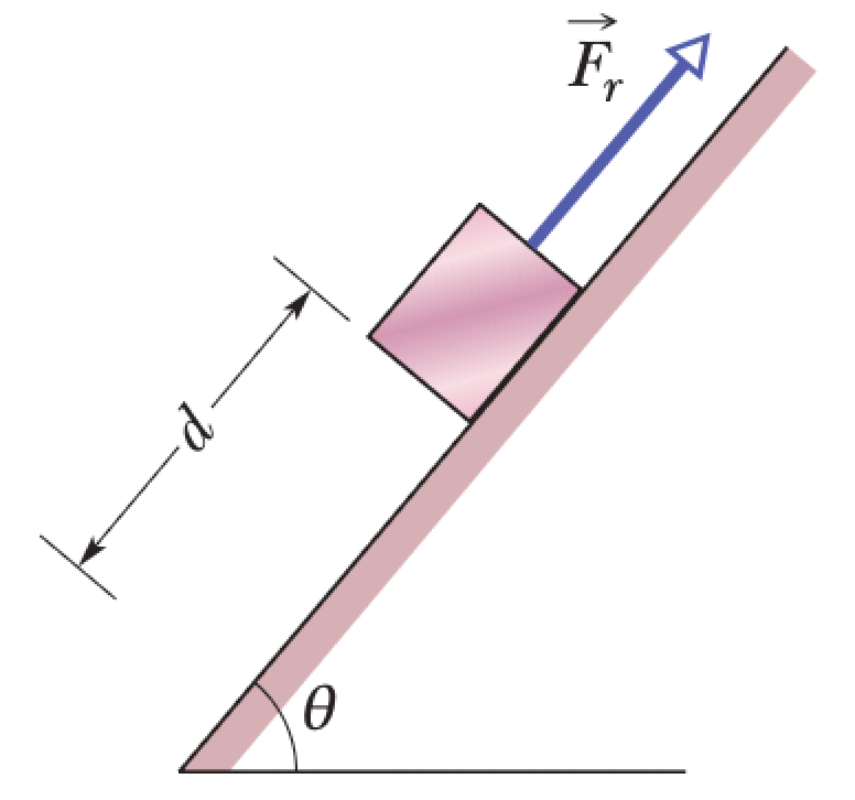
P0543-problem-1
The kinetic energy increase would have been greater by $F_r d$.
According to the work-energy theorem, the net work done on an object equals its change in kinetic energy, $W_{net} = \Delta K$.
Let's first consider the case with the rope attached. The forces doing work are the component of gravity along the ramp, $F_g = mg \sin\theta$, and the rope force $F_r$. The displacement is $d$ down the ramp. The work done by gravity is $W_g = (mg \sin\theta)d$. The work done by the rope is $W_r = -F_r d$, since the force is opposite to the direction of displacement. The net work is $W_{net} = W_g + W_r = (mg \sin\theta)d - F_r d$. The change in kinetic energy is given as $\Delta K = W_{net}$.
$$ \Delta K = (mg \sin\theta)d - F_r d $$Now, consider the case without the rope. The only force doing work along the ramp is gravity. The net work in this case is $W_{net}' = W_g = (mg \sin\theta)d$. The new change in kinetic energy would be $\Delta K' = W_{net}'$.
$$ \Delta K' = (mg \sin\theta)d $$The question asks for how much greater the kinetic energy increase would have been, which is the difference $\Delta K' - \Delta K$.
$$ \Delta K' - \Delta K = [(mg \sin\theta)d] - [(mg \sin\theta)d - F_r d] $$ $$ \Delta K' - \Delta K = F_r d $$The increase in kinetic energy is greater by an amount equal to the magnitude of the work done by the rope.