Source: Principles of Physics
Problem Sets:
Problem
A spring-loaded gun is mounted horizontally on a table. A child tries to hit a small target box on the floor, located a horizontal distance $D$ from the edge of the table. In the first attempt, the spring is compressed by a distance $x_1$, and the marble falls short of the center of the box by a distance $S_1$. Assume no friction.
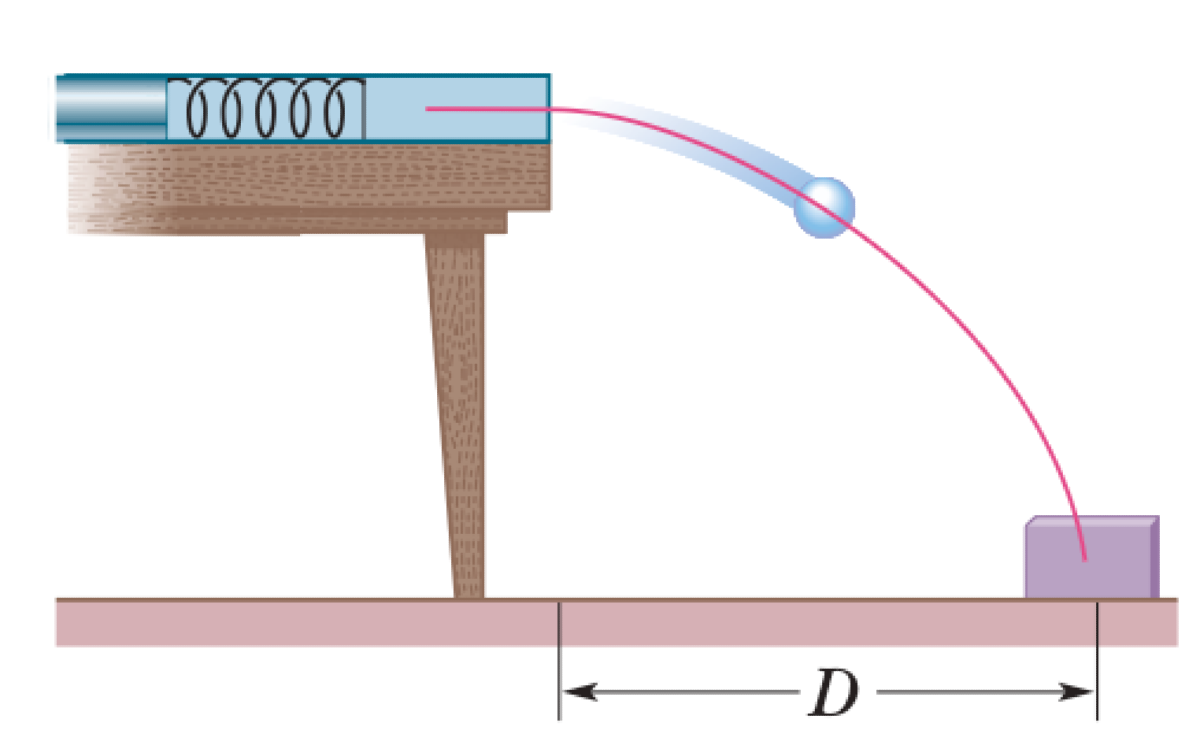
P0541-problem-1
[Q1] $x_2 = x_1 \left( \frac{D}{D-S_1} \right)$
Let the mass of the marble be $m$ and the spring constant be $k$. The height of the table is $h$.
First, relate the launch speed $v$ to the spring compression $x$ using conservation of energy. The initial spring potential energy is converted into kinetic energy of the marble.
$$\frac{1}{2}kx^2 = \frac{1}{2}mv^2 \implies v = x\sqrt{\frac{k}{m}}$$The launch speed is directly proportional to the compression, $v \propto x$.
Next, analyze the projectile motion. The time of flight $t_f$ depends only on the table height $h$ and gravity $g$, and is found from the vertical motion: $h = \frac{1}{2}gt_f^2$. The time $t_f = \sqrt{2h/g}$ is the same for both attempts.
The horizontal range $R$ is given by $R = v t_f$. Since $t_f$ is constant, the range is directly proportional to the launch speed, $R \propto v$.
Combining the proportionalities, we find that the range is directly proportional to the spring compression: $R \propto x$. We can set up a ratio for the two attempts:
$$\frac{R_2}{R_1} = \frac{x_2}{x_1}$$The range of the first attempt is $R_1 = D - S_1$. The desired range for the second attempt is $R_2 = D$. Substituting these into the ratio:
$$\frac{D}{D-S_1} = \frac{x_2}{x_1}$$Solving for the required compression $x_2$:
$$x_2 = x_1 \left( \frac{D}{D-S_1} \right)$$