Source: Principles of Physics
Problem Sets:
Problem
A spring with constant $k$ is at the top of a frictionless incline of angle $\theta$. The lower end of the incline is a distance $D$ from the spring's relaxed position. A canister of mass $m$ is pushed against the spring until it is compressed by a distance $x$ and released from rest.
- What is the speed of the canister, $v_1$, at the instant the spring returns to its relaxed length?
- What is the speed of the canister, $v_2$, when it reaches the lower end of the incline?
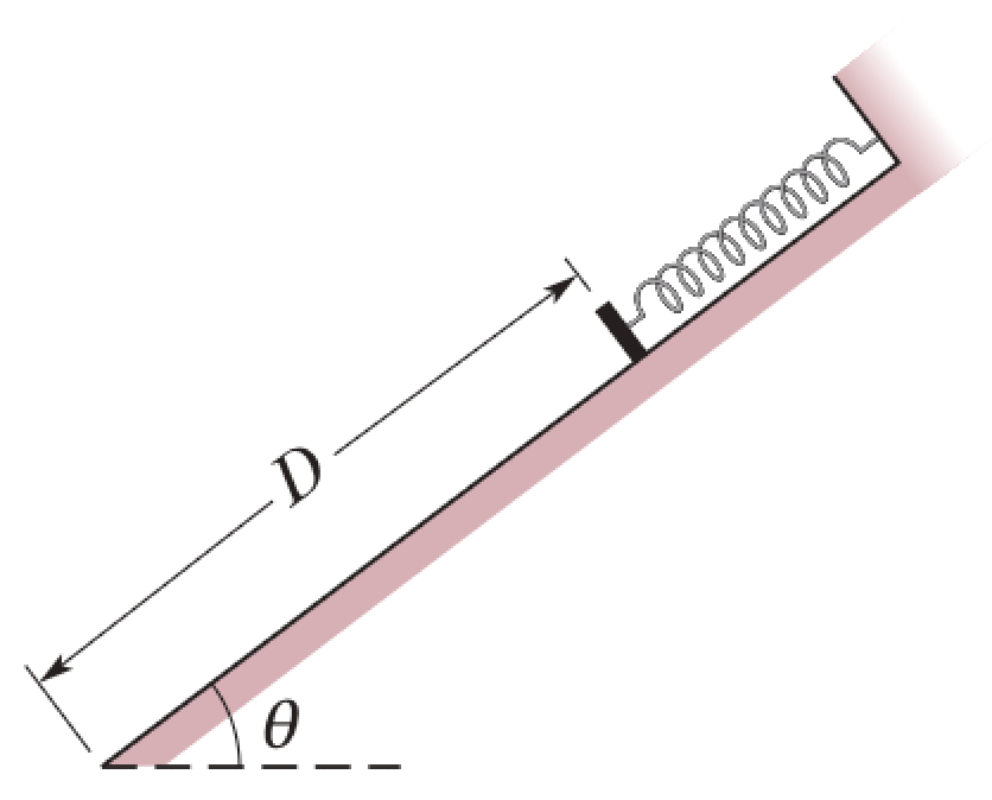
P0538-problem-1
[Q1] $v_1 = \sqrt{\frac{kx^2}{m} + 2gx\sin\theta}$ [Q2] $v_2 = \sqrt{\frac{kx^2}{m} + 2g(x+D)\sin\theta}$
We use the principle of conservation of mechanical energy. Let the initial position (spring compressed by $x$) be the reference height, $h=0$.
[Q1] The initial energy is purely elastic potential energy, $E_0 = \frac{1}{2}kx^2$. When the spring returns to its relaxed length, the canister has moved a distance $x$ down the incline, so its height has changed by $\Delta h_1 = -x \sin\theta$. The energy at this point is $E_1 = \frac{1}{2}mv_1^2 + mg\Delta h_1 = \frac{1}{2}mv_1^2 - mgx\sin\theta$. By energy conservation, $E_0 = E_1$:
$$\frac{1}{2}kx^2 = \frac{1}{2}mv_1^2 - mgx\sin\theta$$ $$v_1 = \sqrt{\frac{kx^2}{m} + 2gx\sin\theta}$$[Q2] To find the speed at the bottom, we compare the initial state (state 0) with the final state at the bottom of the incline (state 2). The total distance traveled along the incline is $x+D$, and the total change in height is $\Delta h_2 = -(x+D)\sin\theta$. The energy at the bottom is $E_2 = \frac{1}{2}mv_2^2 + mg\Delta h_2 = \frac{1}{2}mv_2^2 - mg(x+D)\sin\theta$. By energy conservation, $E_0 = E_2$:
$$\frac{1}{2}kx^2 = \frac{1}{2}mv_2^2 - mg(x+D)\sin\theta$$ $$v_2 = \sqrt{\frac{kx^2}{m} + 2g(x+D)\sin\theta}$$