Source: Principles of Physics
Problem Sets:
Problem
A particle can slide along a track with elevated ends and a flat central part, as shown in Figure. The flat part has length $L = 40$ cm. The curved portions of the track are frictionless, but for the flat part the coefficient of kinetic friction is $\mu_k = 0.20$. The particle is released from rest at point A, which is at height $h = L/2$.
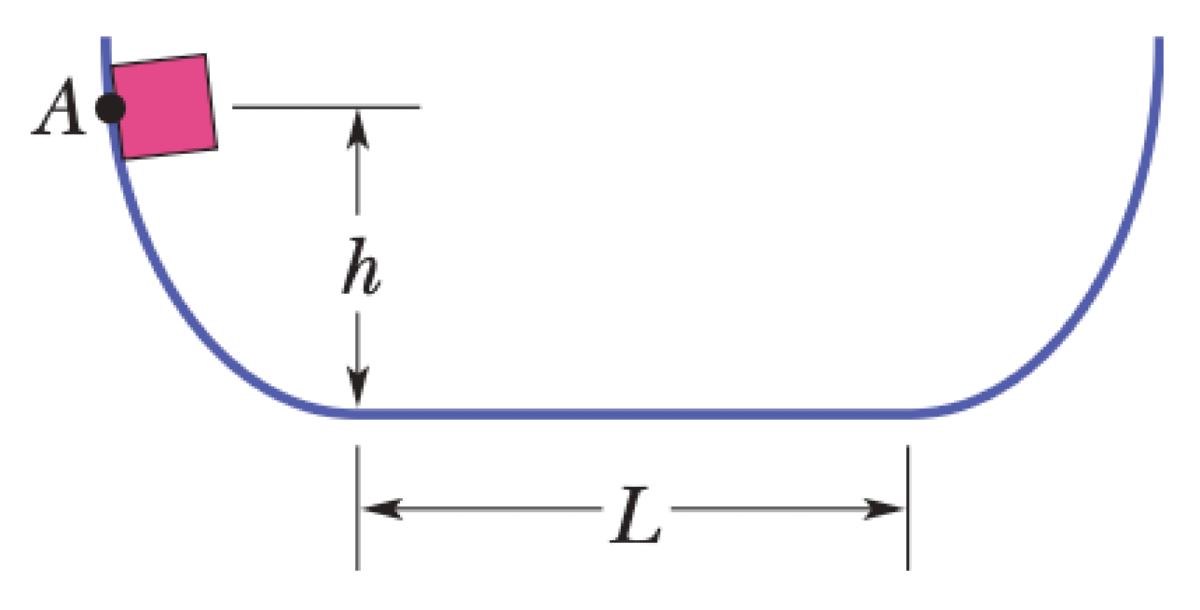
P0537-problem-1
d = 20 cm
The particle's initial mechanical energy is entirely potential, $E_i = mgh$. The particle will come to rest on the flat part, so its final mechanical energy is $E_f = 0$. The change in mechanical energy is due to the work done by friction, $W_f$.
Let $d_{total}$ be the total distance the particle slides on the flat part. The work done by friction is $W_f = -f_k d_{total} = -\mu_k N d_{total} = -\mu_k mg d_{total}$.
Using the work-energy theorem, $\Delta E = E_f - E_i = W_f$:
$$0 - mgh = -\mu_k mg d_{total}$$ $$d_{total} = \frac{h}{\mu_k}$$Given $h = L/2$, the total distance traveled on the flat part is:
$$d_{total} = \frac{L/2}{\mu_k} = \frac{L}{2\mu_k}$$ $$d_{total} = \frac{40 \text{ cm}}{2(0.20)} = \frac{40 \text{ cm}}{0.40} = 100 \text{ cm}$$The particle slides across the flat part of length $L = 40$ cm.
- First pass (left to right): travels 40 cm.
- Second pass (right to left): travels 40 cm. Total distance is $40 + 40 = 80$ cm.
- Third pass (left to right): travels the remaining distance $100 - 80 = 20$ cm.
The particle stops 20 cm from the left edge of the flat part.