Source: Principles of Physics
Problem
A small block is sent through point A with a speed of $v_A = 7.0$ m/s. Its path is frictionless until it reaches point C. The section from C to D has length $L = 12$ m and a coefficient of kinetic friction $\mu_k = 0.70$. The heights are $h_1 = 6.0$ m and $h_2 = 2.0$ m, relative to the lowest point B.
- What is the speed of the block at point B?
- What is the speed of the block at point C?
- Does the block reach point D? If so, what is its speed there? If not, how far through the section of friction does it travel?
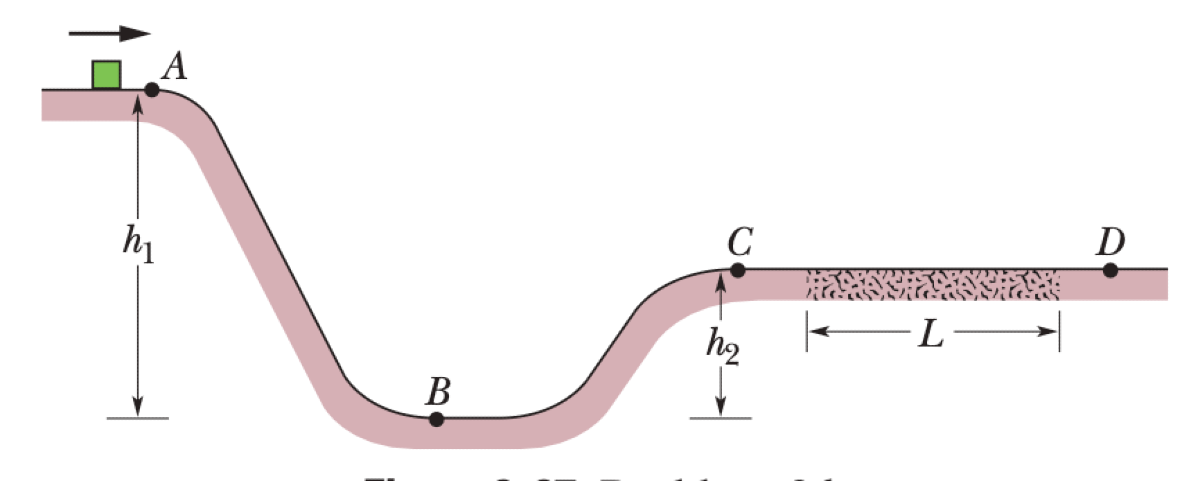
P0535-problem-1
[Q1] $v_B = 13$ m/s [Q2] $v_C = 11$ m/s [Q3] The block does not reach point D. It travels 9.3 m into the friction section.
Set the potential energy reference $U=0$ at the lowest point B.
[Q1] Apply the conservation of mechanical energy between A and B, where the path is frictionless.
$$K_A + U_A = K_B + U_B$$ $$\frac{1}{2}mv_A^2 + mgh_1 = \frac{1}{2}mv_B^2 + 0$$Solving for $v_B$:
$$v_B = \sqrt{v_A^2 + 2gh_1}$$ $v_B = \sqrt{(7.0 \text{ m/s})^2 + 2(9.8 \text{ m/s}^2)(6.0 \text{ m})} = 12.9$ m/s.[Q2] Apply the conservation of mechanical energy between A and C, which is also a frictionless path.
$$K_A + U_A = K_C + U_C$$ $$\frac{1}{2}mv_A^2 + mgh_1 = \frac{1}{2}mv_C^2 + mgh_2$$Solving for $v_C$:
$$v_C = \sqrt{v_A^2 + 2g(h_1 - h_2)}$$ $v_C = \sqrt{(7.0 \text{ m/s})^2 + 2(9.8 \text{ m/s}^2)(6.0 \text{ m} - 2.0 \text{ m})} = 11.3$ m/s.[Q3] On the rough section from C, friction does negative work $W_f = -f_k d = -\mu_k mgd$. To find the stopping distance $d$, we use the work-energy theorem. The block's kinetic energy at C is converted into thermal energy by friction.
$$\Delta E_{mech} = W_f$$ $$(K_{final} - K_C) + (U_{final} - U_C) = -\mu_k mgd$$At stopping, $K_{final}=0$. Since the path is horizontal, $U_{final} = U_C$.
$$0 - \frac{1}{2}mv_C^2 = -\mu_k mgd$$ $$d = \frac{v_C^2}{2\mu_k g}$$Using $v_C^2 = 127.4 \text{ m}^2/\text{s}^2$ from part (b):
$d = \frac{127.4 \text{ m}^2/\text{s}^2}{2(0.70)(9.8 \text{ m/s}^2)} = 9.3$ m.Since $d = 9.3$ m is less than $L = 12$ m, the block does not reach point D.