Source: Principles of Physics
Problem Sets:
Problem
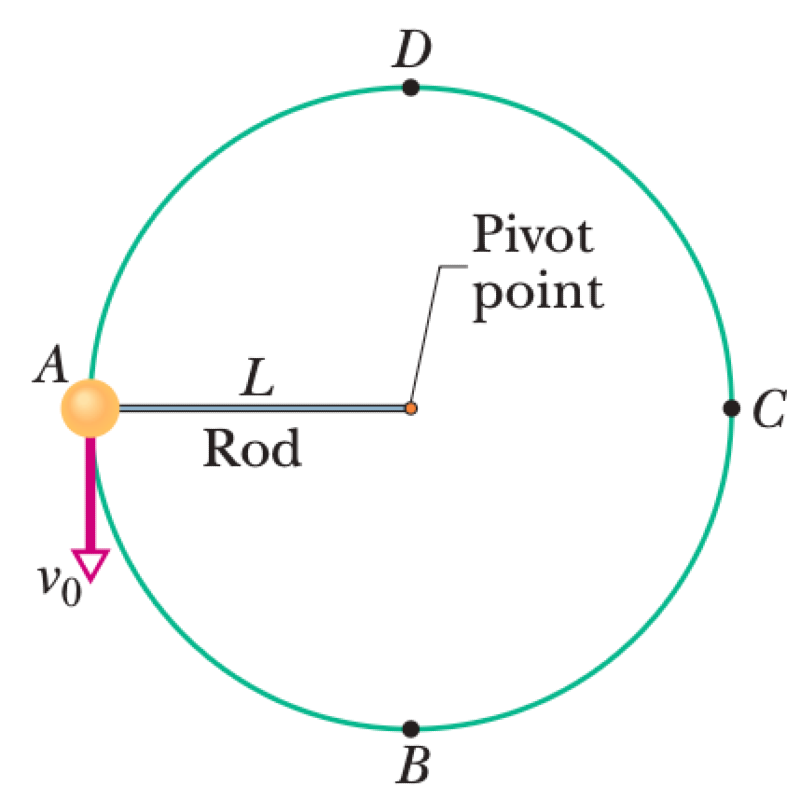
A massless rigid rod of length $L$ has a ball of mass $m$ attached to one end. The other end is pivoted so that the ball moves in a vertical circle. First, assume there is no friction at the pivot. The system is launched downward from the horizontal position A with an initial speed $v_0$. The ball just barely reaches point D (the top) and then stops.
- Derive an expression for $v_0$ in terms of $L$, $m$, and $g$.
- What is the tension in the rod when the ball passes through B (the bottom)?
- A little grit is placed on the pivot to increase the friction there. The ball just barely reaches C when launched from A with the same speed as before. What is the decrease in the mechanical energy during this motion?
- What is the decrease in the mechanical energy by the time the ball finally comes to rest at B after several oscillations?
P0534-problem-1
[Q1] $v_0 = \sqrt{2gL}$ [Q2] $T_B = 5mg$ [Q3] Decrease in energy is $mgL$. [Q4] Decrease in energy is $2mgL$.
Let the potential energy $U$ be zero at the level of the pivot (points A and C). The radius of the circle is $L$.
[Q1] Apply the principle of conservation of mechanical energy between A and D. The ball "just barely reaches D" means its speed at D is $v_D=0$.
$$E_A = E_D \implies K_A + U_A = K_D + U_D$$ $$\frac{1}{2}mv_0^2 + 0 = 0 + mgL$$ $$v_0 = \sqrt{2gL}$$[Q2] First, find the speed at B, $v_B$, using conservation of energy between A and B.
$$E_A = E_B \implies K_A + U_A = K_B + U_B$$ $$\frac{1}{2}mv_0^2 + 0 = \frac{1}{2}mv_B^2 - mgL$$Substitute $v_0^2 = 2gL$ from part (a):
$$mgL = \frac{1}{2}mv_B^2 - mgL \implies v_B^2 = 4gL$$At point B, the net force provides the centripetal acceleration, $a_c = v_B^2/L$. Applying Newton's second law in the vertical direction:
$$\sum F_y = T_B - mg = m \frac{v_B^2}{L}$$ $$T_B = mg + m \frac{4gL}{L} = 5mg$$[Q3] With friction, the mechanical energy is not conserved. The decrease in mechanical energy equals the work done by friction, $W_{nc}$. The ball "just barely reaches C", so $v_C=0$.
$$\Delta E = E_C - E_A = (K_C + U_C) - (K_A + U_A)$$ $$\Delta E = (0 + 0) - (\frac{1}{2}mv_0^2 + 0)$$Using $v_0^2 = 2gL$, the initial energy is $E_A = mgL$.
$$\Delta E = -mgL$$The decrease in mechanical energy is $|\Delta E| = mgL$.
[Q4] The system starts at A and comes to rest at B. Initial energy at A: $E_A = K_A + U_A = \frac{1}{2}mv_0^2 + 0 = mgL$. Final energy at B (at rest): $E_{B, final} = K_{B, final} + U_B = 0 - mgL = -mgL$. The total decrease in mechanical energy is the difference between the initial and final energy.
$$\text{Decrease} = E_A - E_{B, final} = mgL - (-mgL) = 2mgL$$