Source: Principles of Physics
Problem
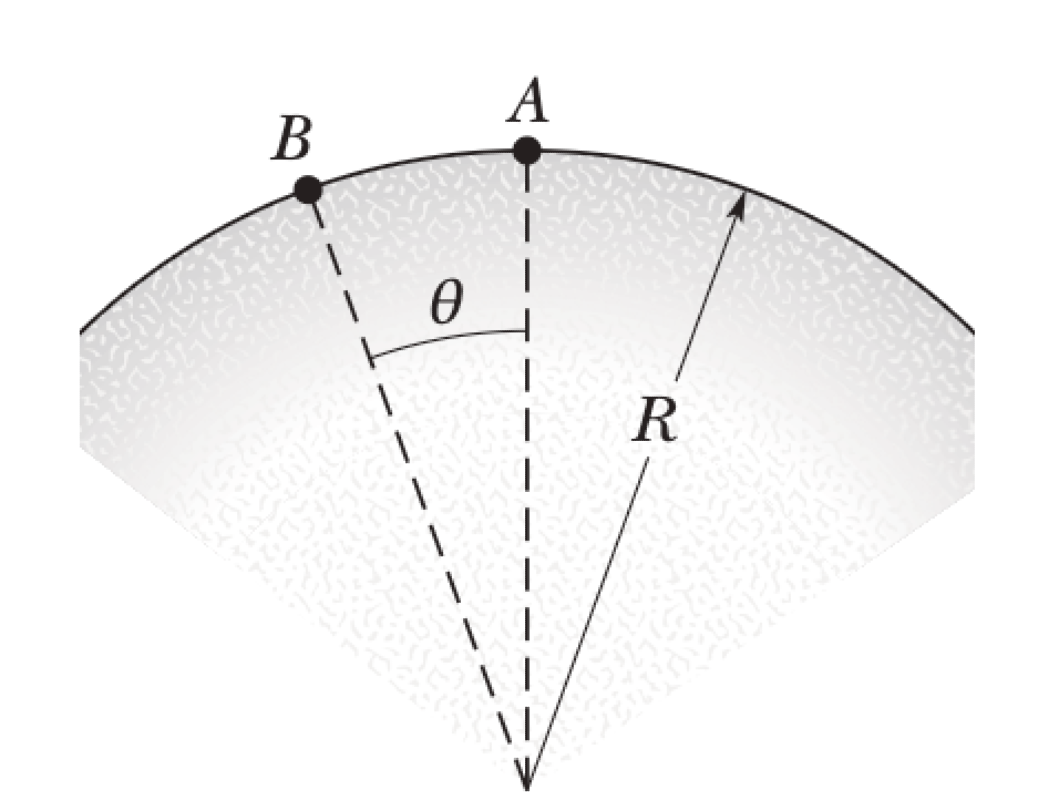
A skier weighing 600 N goes over a frictionless circular hill of radius $R = 20$ m. Assume that the effects of air resistance on the skier are negligible. As she comes up the hill, her speed is 8.0 m/s at point $B$, at an angle $\theta = 20^\circ$.
- What is her speed at the hilltop (point A) if she coasts without using her poles?
- What minimum speed can she have at $B$ and still coast to the hilltop?
- Do the answers to these two questions increase, decrease, or remain the same if the skier weighs 700 N instead of 600 N?
P0532-problem-1
[Q1] $v_A = 6.4$ m/s [Q2] $v_{B,min} = 4.9$ m/s [Q3] Remain the same.
The mechanical energy of the skier is conserved as she moves from point B to A because the hill is frictionless and air resistance is negligible. Let the gravitational potential energy be zero at the center of the circular path. The heights of points A and B are $h_A = R$ and $h_B = R \cos\theta$.
The conservation of energy equation is:
$$K_B + U_B = K_A + U_A$$ $$\frac{1}{2}mv_B^2 + mg(R\cos\theta) = \frac{1}{2}mv_A^2 + mgR$$The mass $m$ cancels out, indicating the results are independent of the skier's weight.
$$v_A^2 = v_B^2 + 2gR(\cos\theta - 1) = v_B^2 - 2gR(1 - \cos\theta)$$[Q1] The speed at the hilltop, $v_A$, can be found by substituting the given values.
$$v_A = \sqrt{v_B^2 - 2gR(1 - \cos\theta)}$$[Q2] To find the minimum speed at B, $v_{B,min}$, we set the condition that the skier just reaches the top, meaning her speed at A is zero ($v_A = 0$).
$$0 = v_{B,min}^2 - 2gR(1 - \cos\theta)$$ $$v_{B,min} = \sqrt{2gR(1 - \cos\theta)}$$[Q3] Since the mass $m$ was eliminated from all equations for speed, the answers are independent of the skier's weight. Therefore, the answers will remain the same.