Source: Principles of Physics
Problem
An 1800 kg elevator cab's cable snaps when it is at rest. The cab bottom is a distance $d = 3.7$ m above a spring with a spring constant of $k = 0.15$ MN/m. A safety device provides a constant frictional force of $f_k = 4.4$ kN that opposes the cab's motion.
- Find the speed of the cab just before it hits the spring.
- Find the maximum distance $x$ that the spring is compressed.
- Find the distance that the cab will bounce back up the shaft.
- Using conservation of energy, find the approximate total distance the cab will move before coming to rest.
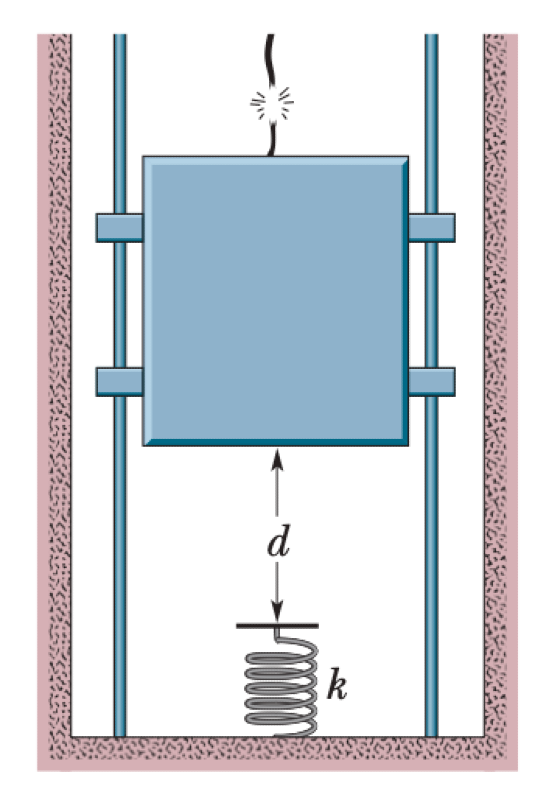
P0530-problem-1
[Q1] v = 7.4 m/s [Q2] x = 0.90 m [Q3] y_{up} = 2.8 m [Q4] D_{total} = 15 m
The principle of conservation of energy, including the work done by the non-conservative frictional force, is used. The work-energy theorem states that the change in mechanical energy is equal to the work done by non-conservative forces: $\Delta E_{mech} = W_{nc}$. Let $m = 1800$ kg, $d = 3.7$ m, $k = 0.15 \times 10^6$ N/m, and $f_k = 4400$ N.
[Q1] Let the top of the uncompressed spring be the zero for gravitational potential energy. The cab starts from rest at height $d$ and falls to height 0. The change in mechanical energy equals the work done by friction.
$$ (K_f + U_f) - (K_i + U_i) = -f_k d $$ $$ (\frac{1}{2}mv^2 + 0) - (0 + mgd) = -f_k d $$ $$ \frac{1}{2}mv^2 = mgd - f_k d $$ $$ v = \sqrt{\frac{2(mg - f_k)d}{m}} $$[Q2] The cab starts from rest at height $d$ above the spring and comes to rest when the spring is compressed by a maximum distance $x$. The total distance fallen is $d+x$.
$$ \Delta E_{mech} = W_{nc} $$ $$ E_f - E_i = -f_k (d+x) $$Let the final position (max compression) be the zero for gravitational potential energy. The initial height is $d+x$.
$$ (\frac{1}{2}kx^2 + 0) - (0 + mg(d+x)) = -f_k(d+x) $$ $$ \frac{1}{2}kx^2 - (mg - f_k)x - (mg - f_k)d = 0 $$This is a quadratic equation for $x$. We solve for the positive root.
[Q3] The cab starts from rest at maximum compression $x$ and travels up a distance $y_{up}$, coming to rest again. Let the lowest point be the potential energy zero.
$$ \Delta E_{mech} = W_{nc} $$ $$ (mgy_{up} + 0) - (0 + \frac{1}{2}kx^2) = -f_k y_{up} $$ $$ y_{up}(mg + f_k) = \frac{1}{2}kx^2 $$ $$ y_{up} = \frac{kx^2}{2(mg+f_k)} $$[Q4] The cab starts at rest at height $d$ and eventually comes to rest at the equilibrium position where the spring force balances gravity, $kx_{eq} = mg$. Let $D_{total}$ be the total distance moved. The total work done by friction equals the total change in mechanical energy.
$$ W_{nc} = E_f - E_i $$Let the initial position be the zero for gravitational potential energy. The final position is at $-(d+x_{eq})$.
$$ -f_k D_{total} = (\frac{1}{2}kx_{eq}^2 + mg(-(d+x_{eq}))) - 0 $$Substitute $mg = kx_{eq}$:
$$ -f_k D_{total} = \frac{1}{2}k(\frac{mg}{k})^2 - mgd - mg(\frac{mg}{k}) = \frac{(mg)^2}{2k} - mgd - \frac{(mg)^2}{k} $$ $$ -f_k D_{total} = -mgd - \frac{(mg)^2}{2k} $$ $$ D_{total} = \frac{mgd + (mg)^2/(2k)}{f_k} $$