Source: Principles of Physics
Problem
Figure applies to the spring in a cork gun; it shows the spring force as a function of the stretch or compression of the spring. The spring is compressed by 5.5 cm and used to propel a 3.8 g cork from the gun.
- What is the speed of the cork if it is released as the spring passes through its relaxed position?
- Suppose, instead, that the cork sticks to the spring and stretches it 1.5 cm before separation occurs. What now is the speed of the cork at the time of release?
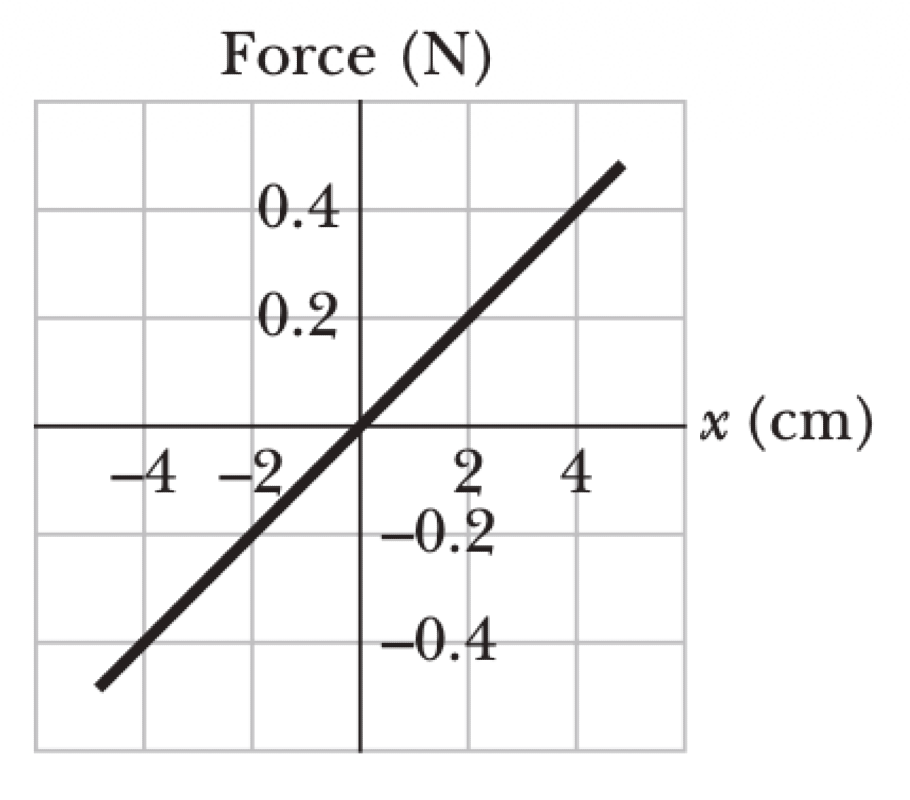
P0527-problem-1
[Q1] v = 2.8 m/s [Q2] v = 2.7 m/s
The spring constant $k$ is the slope of the force-displacement graph.
$$k = \frac{\Delta F}{\Delta x} = \frac{0.4 \text{ N}}{0.04 \text{ m}} = 10 \text{ N/m}$$The problem is solved using the conservation of mechanical energy, where the initial energy is the potential energy stored in the compressed spring. Let the initial compression be $x_i = 0.055$ m and the mass of the cork be $m = 0.0038$ kg.
[Q1] The initial energy is $E_i = \frac{1}{2}kx_i^2$. The final energy, when the spring is at its relaxed position ($x_f = 0$), is purely kinetic, $E_f = \frac{1}{2}mv^2$.
$$ \frac{1}{2}kx_i^2 = \frac{1}{2}mv^2 $$ $$ v = x_i \sqrt{\frac{k}{m}} = 0.055 \text{ m} \sqrt{\frac{10 \text{ N/m}}{0.0038 \text{ kg}}} $$[Q2] The initial energy is the same, $E_i = \frac{1}{2}kx_i^2$. The final state occurs when the spring is stretched by $x_f = 0.015$ m. The final energy is a sum of the spring's potential energy and the cork's kinetic energy, $E_f = \frac{1}{2}kx_f^2 + \frac{1}{2}mv^2$.
$$ \frac{1}{2}kx_i^2 = \frac{1}{2}kx_f^2 + \frac{1}{2}mv^2 $$ $$ v = \sqrt{\frac{k(x_i^2 - x_f^2)}{m}} = \sqrt{\frac{10 \text{ N/m}((0.055 \text{ m})^2 - (0.015 \text{ m})^2)}{0.0038 \text{ kg}}} $$