Source: Principles of Physics
Problem Sets:
Problem
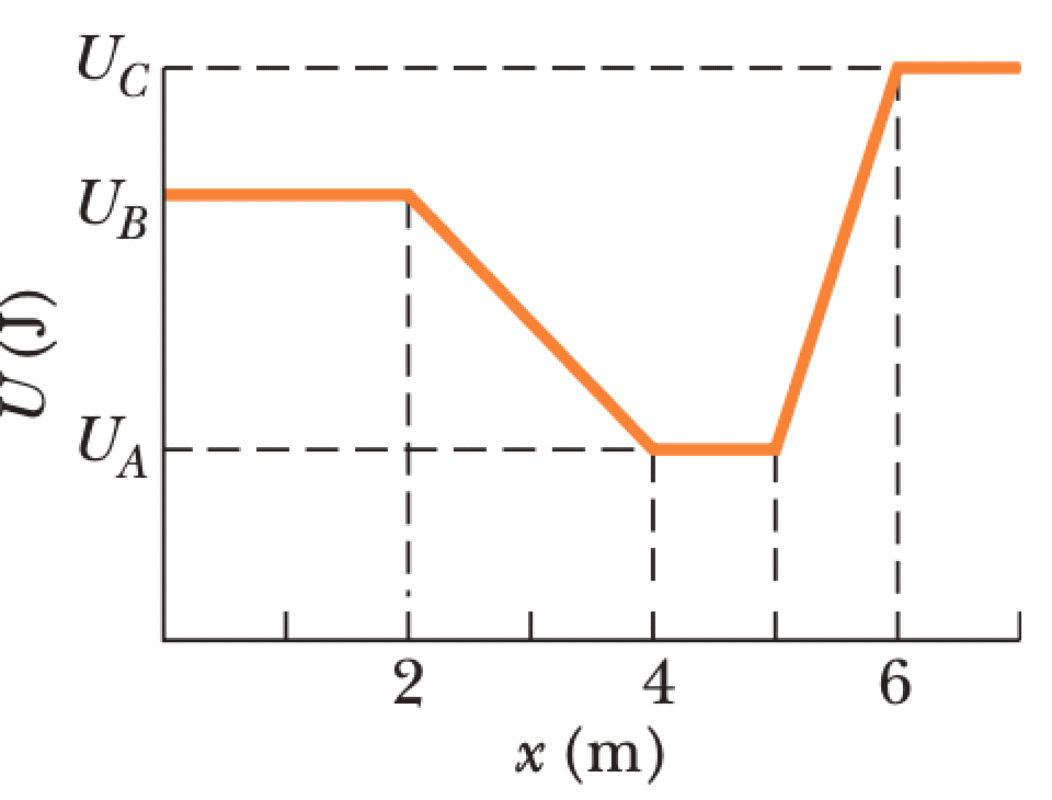
Figure shows a plot of potential energy $U$ versus position $x$ of a 0.90 kg particle that can travel only along an x axis. (Nonconservative forces are not involved.) Three values are $U_A = 15.0$ J, $U_B = 35.0$ J, and $U_C = 45.0$ J. The particle is released at $x = 4.5$ m with an initial speed of 7.0 m/s, headed in the negative x direction.
- If the particle can reach $x = 1.0$ m, what is its speed there, and if it cannot, what is its turning point?
- What is the magnitude of the force on the particle as it begins to move to the left of $x = 4.0$ m?
- What is the direction of the force in Q2?
- Suppose, instead, the particle is headed in the positive x direction when it is released at $x = 4.5$ m at speed 7.0 m/s. If the particle can reach $x = 7.0$ m, what is its speed there, and if it cannot, what is its turning point?
- What is the magnitude of the force on the particle as it begins to move to the right of $x = 5.0$ m?
- What is the direction of the force in Q5?
P0526-problem-1
[Q1] v = 2.1 m/s [Q2] F = 10 N [Q3] positive x direction [Q4] x = 5.7 m [Q5] F = 30 N [Q6] negative x direction
The total mechanical energy $E_{mech}$ of the particle is conserved. The initial position is $x_i = 4.5$ m and initial speed is $v_i = 7.0$ m/s. From the graph, the potential energy at the start is $U(x_i) = U_A = 15.0$ J. The initial kinetic energy is $K_i = \frac{1}{2}mv_i^2 = \frac{1}{2}(0.90 \text{ kg})(7.0 \text{ m/s})^2 = 22.05$ J. The total mechanical energy is $E_{mech} = K_i + U_i = 22.05 \text{ J} + 15.0 \text{ J} = 37.05$ J.
[Q1] At $x_f = 1.0$ m, the potential energy is $U(x_f) = U_B = 35.0$ J. Since $E_{mech} = 37.05 \text{ J} > U_B$, the particle can reach $x = 1.0$ m. By conservation of energy, $E_{mech} = K_f + U(x_f)$.
$$K_f = E_{mech} - U(x_f) = 37.05 \text{ J} - 35.0 \text{ J} = 2.05 \text{ J}$$ $$v_f = \sqrt{\frac{2K_f}{m}} = \sqrt{\frac{2(2.05 \text{ J})}{0.90 \text{ kg}}} \approx 2.1 \text{ m/s}$$[Q2] & [Q3] The force is given by $F_x = -dU/dx$. For the region $2 < x < 4$ m:
$$F_x = -\frac{\Delta U}{\Delta x} = -\frac{U_A - U_B}{4.0 \text{ m} - 2.0 \text{ m}} = -\frac{15.0 \text{ J} - 35.0 \text{ J}}{2.0 \text{ m}} = 10 \text{ N}$$The magnitude is 10 N, and the direction is positive x.
[Q4] At $x_f = 7.0$ m, the potential energy is $U(x_f) = U_C = 45.0$ J. Since $E_{mech} = 37.05 \text{ J} < U_C$, the particle cannot reach $x = 7.0$ m. The turning point $x_t$ occurs where $K=0$, so $U(x_t) = E_{mech} = 37.05$ J. This occurs on the slope between $x=5$ m and $x=6$ m. The equation for potential energy in this region is $U(x) = U_A + \frac{U_C-U_A}{6-5}(x-5) = 15.0 + 30.0(x-5)$.
$$37.05 = 15.0 + 30.0(x_t - 5)$$ $$x_t = 5 + \frac{37.05 - 15.0}{30.0} \approx 5.7 \text{ m}$$[Q5] & [Q6] For the region $5 < x < 6$ m:
$$F_x = -\frac{\Delta U}{\Delta x} = -\frac{U_C - U_A}{6.0 \text{ m} - 5.0 \text{ m}} = -\frac{45.0 \text{ J} - 15.0 \text{ J}}{1.0 \text{ m}} = -30 \text{ N}$$The magnitude is 30 N, and the direction is negative x.