Source: Principles of Physics
Problem Sets:
Problem
A 2.0 kg lunchbox is sent sliding over a frictionless surface in the positive direction of an x axis. Beginning at time $t = 0$, a steady wind pushes on the lunchbox in the negative direction of the x axis. The figure shows the position $x$ of the lunchbox as a function of time $t$.
- From the graph, estimate the kinetic energy of the lunchbox at $t = 1.0$ s.
- From the graph, estimate the kinetic energy of the lunchbox at $t = 5.0$ s.
- How much work does the force from the wind do on the lunchbox from $t = 1.0$ s to $t = 5.0$ s?
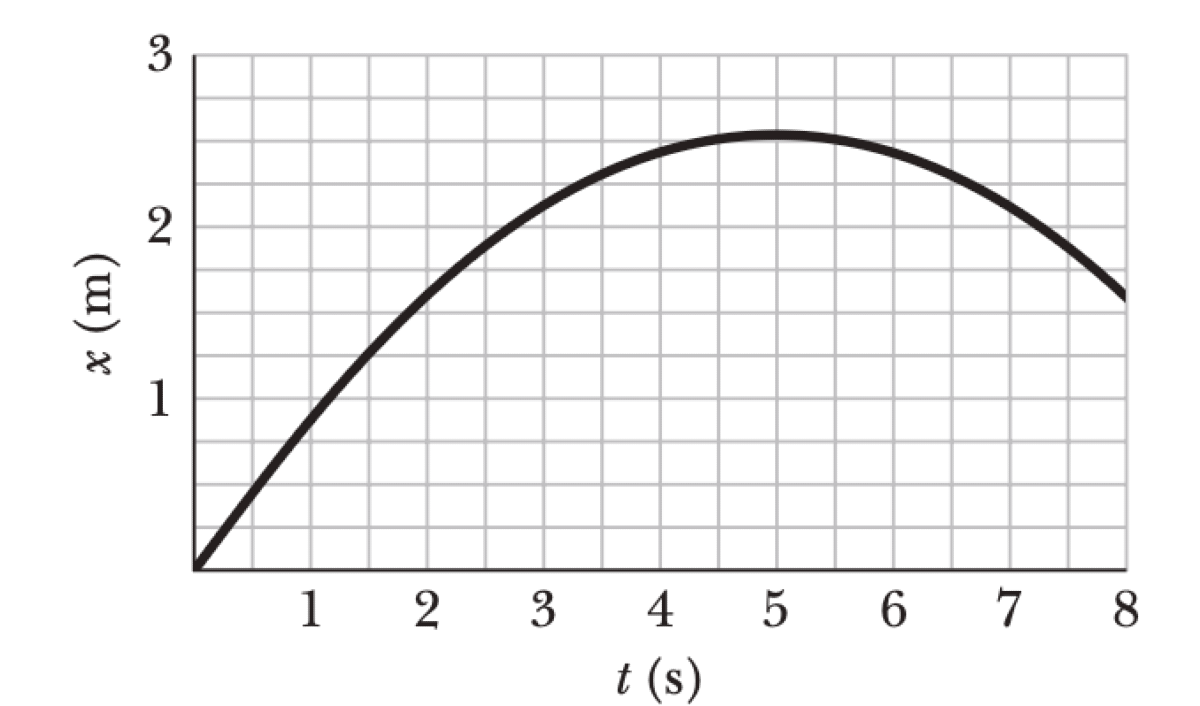
P0524-problem-1
[Q1] $K = 0.64$ J [Q2] $K = 0$ J [Q3] $W = -0.64$ J
The velocity $v$ is the slope of the position-time graph ($v = dx/dt$). The kinetic energy is $K = \frac{1}{2}mv^2$. The work done by the net force (here, the wind) equals the change in kinetic energy, $W_{wind} = \Delta K$.
A "steady wind" implies a constant force and thus constant acceleration, $a$. The position is described by $x(t) = v_0 t + \frac{1}{2} a t^2$. From the graph, the lunchbox reaches its maximum position at $t_p = 5.0$ s, where its velocity is momentarily zero.
$$v(t_p) = v_0 + at_p = 0 \implies v_0 = -at_p = -5.0a$$The position at this time is $x(5.0) \approx 2.5$ m.
$$x(t_p) = v_0 t_p + \frac{1}{2} a t_p^2 = (-at_p)t_p + \frac{1}{2}at_p^2 = -\frac{1}{2}at_p^2$$ $$2.5 = -\frac{1}{2}a(5.0)^2 \implies a = -\frac{2(2.5)}{25} = -0.2 \text{ m/s}^2$$The initial velocity is $v_0 = -5.0a = -5.0(-0.2) = 1.0 \text{ m/s}$. The velocity at any time $t$ is $v(t) = v_0 + at = 1.0 - 0.2t$.
[Q1] At $t_1 = 1.0$ s, the velocity is $v_1 = 1.0 - 0.2(1.0) = 0.8 \text{ m/s}$. The kinetic energy is:
$$K_1 = \frac{1}{2}mv_1^2 = \frac{1}{2}(2.0 \text{ kg})(0.8 \text{ m/s})^2 = 0.64 \text{ J}$$[Q2] At $t_2 = 5.0$ s, the velocity is $v_2 = 1.0 - 0.2(5.0) = 0 \text{ m/s}$. The kinetic energy is:
$$K_2 = \frac{1}{2}mv_2^2 = 0 \text{ J}$$[Q3] Using the work-energy theorem, the work done by the wind is:
$$W_{wind} = \Delta K = K_2 - K_1 = 0 \text{ J} - 0.64 \text{ J} = -0.64 \text{ J}$$