Source: Principles of Physics
Problem
A spring with a pointer is hung next to a scale marked in millimeters. When a package of weight $W_1 = 110$ N is hung, the pointer indicates $x_1 = 40$ mm. When a package of weight $W_2 = 240$ N is hung, the pointer indicates $x_2 = 60$ mm. A third package of unknown weight $W$ is hung, and the pointer indicates $x_3 = 30$ mm.
- Which mark on the scale will the pointer indicate when no package is hung from the spring?
- What is the weight $W$ of the third package?
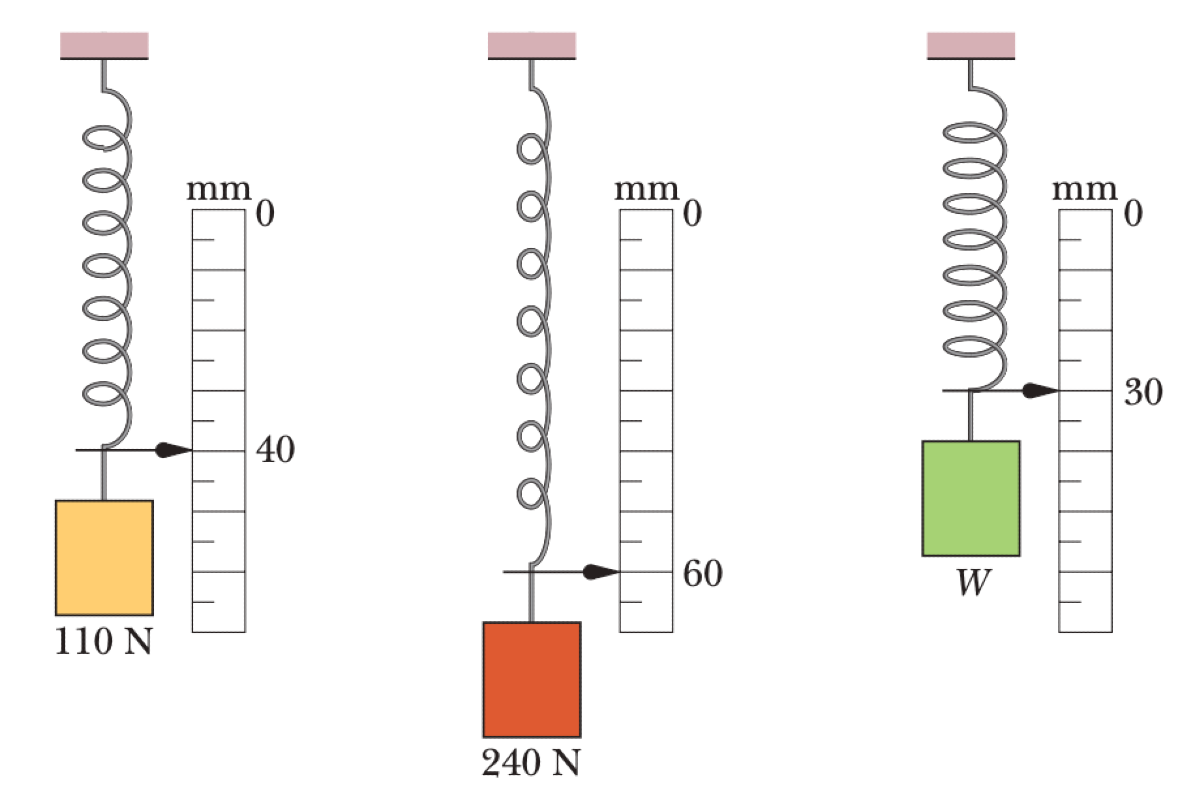
P0523-problem-1
[Q1] $x_0 = 23$ mm [Q2] $W = 45$ N
The weight $W$ hung from the spring is proportional to the spring's extension. Let $x$ be the scale reading and $x_0$ be the reading for the unstretched spring. According to Hooke's Law, $W = k(x - x_0)$, where $k$ is the spring constant.
The spring constant $k$ is the slope of the force vs. position graph, which can be found from the first two data points:
$$k = \frac{\Delta W}{\Delta x} = \frac{W_2 - W_1}{x_2 - x_1}$$ $$k = \frac{240 \text{ N} - 110 \text{ N}}{60 \text{ mm} - 40 \text{ mm}} = \frac{130 \text{ N}}{20 \text{ mm}} = 6.5 \text{ N/mm}$$[Q1] To find the unstretched position $x_0$, we can use the data for the first package, $W_1 = k(x_1 - x_0)$, and solve for $x_0$:
$$x_0 = x_1 - \frac{W_1}{k}$$ $$x_0 = 40 \text{ mm} - \frac{110 \text{ N}}{6.5 \text{ N/mm}} = 40 \text{ mm} - 16.92... \text{ mm} \approx 23 \text{ mm}$$[Q2] The weight $W$ of the third package is found using its measured position $x_3$:
$$W = k(x_3 - x_0)$$Using the unrounded value of $x_0$ for better accuracy ($x_0 = 40 - 110/6.5 = 300/13$ mm):
$$W = (6.5 \text{ N/mm})(30 \text{ mm} - \frac{300}{13} \text{ mm}) = (\frac{13}{2} \frac{\text{N}}{\text{mm}})(\frac{390-300}{13} \text{ mm}) = 45 \text{ N}$$