Source: Principles of Physics
Problem
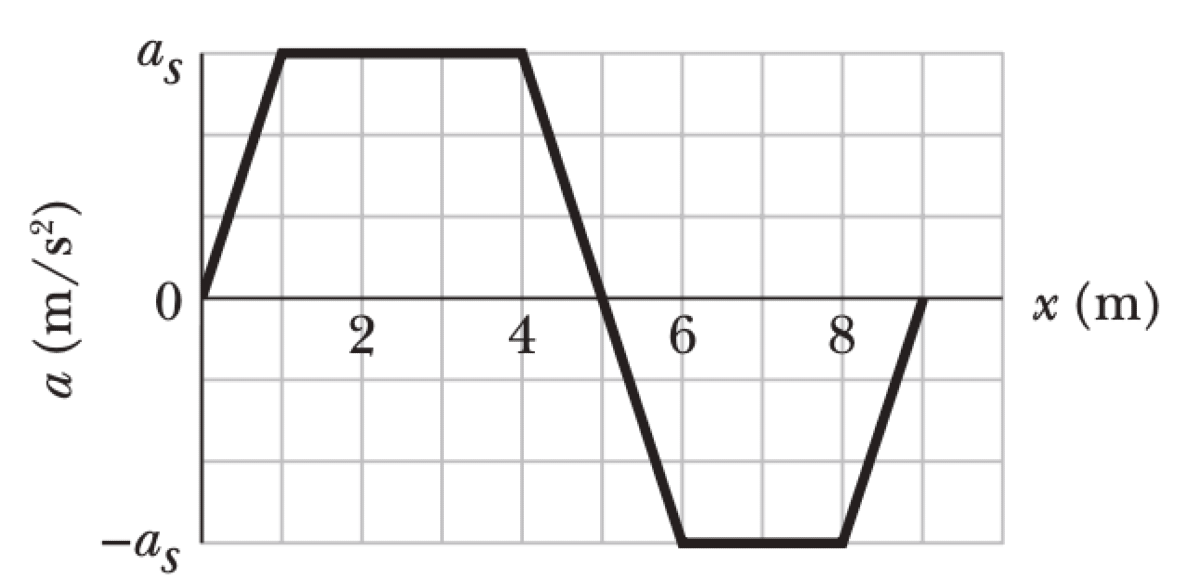
A 2.00 kg particle is moved from rest along an x axis by an applied force. The figure shows the particle's acceleration $a$ versus its position $x$ from $x=0$ to $x=9.0$ m. The vertical axis scale is set by $a_s = 6.0$ m/s$^2$.
- How much work has the force done on the particle when it reaches $x = 4.0$ m?
- How much work has the force done on the particle when it reaches $x = 7.0$ m?
- How much work has the force done on the particle when it reaches $x = 9.0$ m?
- What is the particle's speed and direction of travel when it reaches $x = 4.0$ m?
- What is the particle's speed and direction of travel when it reaches $x = 7.0$ m?
- What is the particle's speed and direction of travel when it reaches $x = 9.0$ m?
P0521-problem-1
[Q1] 42.0 J [Q2] 30.0 J [Q3] 12.0 J [Q4] 6.48 m/s, in the +x direction [Q5] 5.48 m/s, in the +x direction [Q6] 3.46 m/s, in the +x direction
The work done $W$ by the force $\vec{F_a}$ is given by $W = \int F_a dx$. Using Newton's second law, $F_a = ma$, the work can be expressed as:
$$W = \int (ma) dx = m \int a dx$$The integral $\int a dx$ represents the area under the acceleration-position ($a-x$) graph. The work-energy theorem states that the net work done on an object equals its change in kinetic energy, $W = \Delta K = \frac{1}{2}mv_f^2 - \frac{1}{2}mv_i^2$. Since the particle starts from rest, $v_i = 0$, so $W = \frac{1}{2}mv_f^2$. This allows us to find the final speed $v_f$:
$$v_f = \sqrt{\frac{2W}{m}} = \sqrt{2 \int a dx}$$We calculate the area under the $a-x$ graph for each position. Let $A(x) = \int_0^x a dx'$. Area from $x=0$ to $x=4.0$ m: This is a trapezoid, broken into a triangle (0 to 1 m) and a rectangle (1 to 4 m).
$$A(4) = \left(\frac{1}{2} \cdot 1.0 \cdot a_s\right) + \left(3.0 \cdot a_s\right) = 0.5 a_s + 3.0 a_s = 3.5 a_s$$ $$A(4) = 3.5 \cdot (6.0 \text{ m/s}^2) = 21.0 \text{ m}^2\text{/s}^2$$Area from $x=0$ to $x=7.0$ m: We add the area from 4 m to 7 m to $A(4)$. This consists of a positive triangle (4 to 5 m), a negative triangle (5 to 6 m), and a negative rectangle (6 to 7 m).
$$A(7) = A(4) + \left(\frac{1}{2} \cdot 1.0 \cdot a_s\right) + \left(\frac{1}{2} \cdot 1.0 \cdot (-a_s)\right) + \left(1.0 \cdot (-a_s)\right) = A(4) - a_s$$ $$A(7) = 21.0 - 6.0 = 15.0 \text{ m}^2\text{/s}^2$$Area from $x=0$ to $x=9.0$ m: We add the area from 7 m to 9 m to $A(7)$. This consists of a negative rectangle (7 to 8 m) and a negative triangle (8 to 9 m).
$$A(9) = A(7) + \left(1.0 \cdot (-a_s)\right) + \left(\frac{1}{2} \cdot 1.0 \cdot (-a_s)\right) = A(7) - 1.5 a_s$$ $$A(9) = 15.0 - 1.5(6.0) = 15.0 - 9.0 = 6.0 \text{ m}^2\text{/s}^2$$[Q1-Q3] The work done is $W(x) = m \cdot A(x)$:
$W(4) = (2.00 \text{ kg})(21.0 \text{ m}^2\text{/s}^2) = 42.0 \text{ J}$ $W(7) = (2.00 \text{ kg})(15.0 \text{ m}^2\text{/s}^2) = 30.0 \text{ J}$ $W(9) = (2.00 \text{ kg})(6.0 \text{ m}^2\text{/s}^2) = 12.0 \text{ J}$[Q4-Q6] The speed is $v(x) = \sqrt{2 \cdot A(x)}$:
$v(4) = \sqrt{2 \cdot 21.0} = \sqrt{42.0} \approx 6.48 \text{ m/s}$ $v(7) = \sqrt{2 \cdot 15.0} = \sqrt{30.0} \approx 5.48 \text{ m/s}$ $v(9) = \sqrt{2 \cdot 6.0} = \sqrt{12.0} \approx 3.46 \text{ m/s}$Since the cumulative area is always positive, the kinetic energy is always positive and the particle never comes to rest. Therefore, its direction of travel is always in the positive x-direction.