Source: Principles of Physics
Problem
In Figure, a block of mass $m$ lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (spring constant $k$) whose other end is fixed. The block is initially at rest at the position where the spring is unstretched ($x=0$) when a constant horizontal force $\vec{F}$ in the positive direction of the $x$ axis is applied to it. A plot of the resulting kinetic energy of the block versus its position $x$ is shown in Fig. 7-36. The scale of the figure's vertical axis is set by $K_s = 4.0$ J.
- What is the magnitude of $\vec{F}$?
- What is the value of $k$?
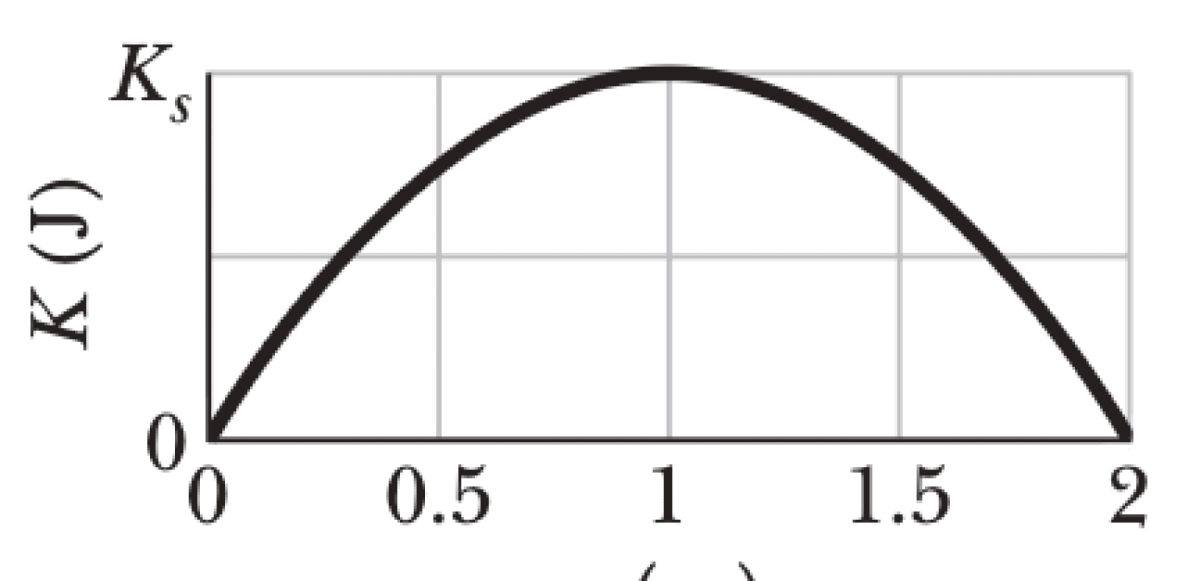
P0520-problem-1
[Q1] $F = 8.0$ N [Q2] $k = 8.0$ N/m
According to the work-energy theorem, the change in kinetic energy $\Delta K$ equals the net work done on the block $W_{net}$. The block starts from rest, so $K_i=0$ and $\Delta K = K(x)$. The net work is the sum of the work done by the applied force $F$ and the work done by the spring.
$$K(x) = W_{net} = W_F + W_s = Fx - \frac{1}{2}kx^2$$From the graph, the kinetic energy is maximum at $x_{maxK} = 1.0$ m. This occurs when the net force on the block is zero. The net force is the sum of the applied force and the spring force: $F_{net} = F - kx$.
$$F_{net} = 0 \implies F - kx_{maxK} = 0$$ $$F = kx_{maxK} = k(1.0 \text{ m}) \implies F=k$$At this position, $x = 1.0$ m, the kinetic energy is $K_{max} = K_s = 4.0$ J. Substituting this into the work-energy equation:
$$K_s = F(1.0) - \frac{1}{2}k(1.0)^2$$Now, substitute $F=k$ into this equation:
$$K_s = k - \frac{1}{2}k = \frac{1}{2}k$$Solving for $k$:
$$k = 2K_s = 2(4.0 \text{ J}) = 8.0 \text{ N/m}$$Since $F=k$, the magnitude of the force is:
$$F = 8.0 \text{ N}$$We can verify this with the point $x=2.0$ m, where $K=0$.
$K(2.0) = F(2.0) - \frac{1}{2}k(2.0)^2 = 2F - 2k = 2(8.0) - 2(8.0) = 0$, which matches the graph.