Source: Physics Competition - Mechanics
Problem
As shown in the figure, a small ball of mass $m$ is launched horizontally from point A with an initial velocity $v_0$. Under the influence of gravity and air resistance, it lands at point B. The velocity at B is $v'_0$, directed at an angle $\theta$ below the horizontal. The air resistance is given by the formula $f = -kv$, where $k$ is a positive constant and $v$ is the ball's velocity.
- Find the magnitude of the final velocity, $v'_0$.
- Find the horizontal distance between A and B, denoted by S.
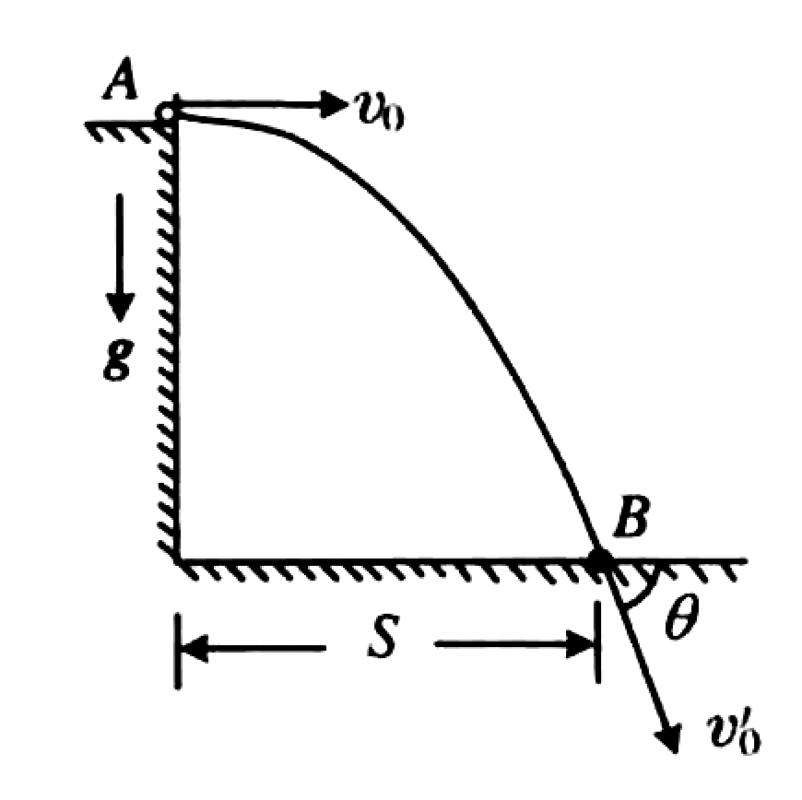
P0515-problem-1
[Q1] $v'_0 = \frac{mgv_0}{kv_0\sin\theta + mg\cos\theta}$ [Q2] $S = \frac{m v_0^2 \sin\theta}{kv_0\sin\theta + mg\cos\theta}$
The equation of motion for the ball is given by Newton's second law:
$$m\frac{d\vec{v}}{dt} = m\vec{g} - k\vec{v}$$Let the terminal velocity be $\vec{v}_T = m\vec{g}/k$. The equation can be rearranged as:
$$m\frac{d}{dt}(\vec{v} - \vec{v}_T) = -k(\vec{v} - \vec{v}_T)$$This shows that the vector $\vec{u}(t) = \vec{v}(t) - \vec{v}_T$ has a rate of change that is always anti-parallel to itself. Therefore, the direction of $\vec{u}(t)$ remains constant throughout the motion and is determined by its initial direction, $\vec{u}(0) = \vec{v}_0 - \vec{v}_T$. This implies that the initial vector $(\vec{v}_0 - \vec{v}_T)$ and the final vector $(\vec{v}'_0 - \vec{v}_T)$ are parallel.
Let's set up a coordinate system with the x-axis horizontal and the y-axis vertically downward. The initial velocity is $\vec{v}_0 = (v_0, 0)$. The final velocity is $\vec{v}'_0 = (v'_0\cos\theta, v'_0\sin\theta)$. The terminal velocity is $\vec{v}_T = (0, mg/k)$.
The initial vector is $(\vec{v}_0 - \vec{v}_T) = (v_0, -mg/k)$. The final vector is $(\vec{v}'_0 - \vec{v}_T) = (v'_0\cos\theta, v'_0\sin\theta - mg/k)$.
Since these two vectors are parallel, their slopes in the velocity plane must be equal:
$$\frac{v'_0\sin\theta - mg/k}{v'_0\cos\theta} = \frac{-mg/k}{v_0}$$Solving for $v'_0$:
$$v_0(v'_0\sin\theta - mg/k) = -v'_0\cos\theta(mg/k)$$ $$v'_0(v_0\sin\theta + \frac{mg}{k}\cos\theta) = \frac{mgv_0}{k}$$ $$v'_0 = \frac{mgv_0}{kv_0\sin\theta + mg\cos\theta}$$To find the horizontal distance S, consider the impulse-momentum theorem in the x-direction. The net horizontal force is $F_x = -kv_x$.
$$\Delta p_x = \int F_x dt$$ $$m(v_{0x}' - v_{0x}) = \int_0^t (-kv_x) dt = -k \int_0^t v_x dt$$The horizontal distance is $S = \int_0^t v_x dt$. Thus:
$$m(v'_0\cos\theta - v_0) = -kS$$ $$S = \frac{m}{k}(v_0 - v'_0\cos\theta)$$Substitute the expression for $v'_0$:
$$S = \frac{m}{k}\left(v_0 - \frac{mgv_0\cos\theta}{kv_0\sin\theta + mg\cos\theta}\right)$$ $$S = \frac{mv_0}{k}\left(\frac{kv_0\sin\theta + mg\cos\theta - mg\cos\theta}{kv_0\sin\theta + mg\cos\theta}\right)$$ $$S = \frac{m v_0^2 \sin\theta}{kv_0\sin\theta + mg\cos\theta}$$