Source: Physics Competition - Mechanics
Problem Sets:
Problem
As shown in the figure, a triangular wedge P of mass $M$ is placed between two blocks Q1 and Q2, of mass $m_1$ and $m_2$ respectively. The blocks can slide on a horizontal plane, and the system is released from rest. The angles between the sides of the wedge and the vertical are $\alpha$ and $\beta$. All surfaces are frictionless.
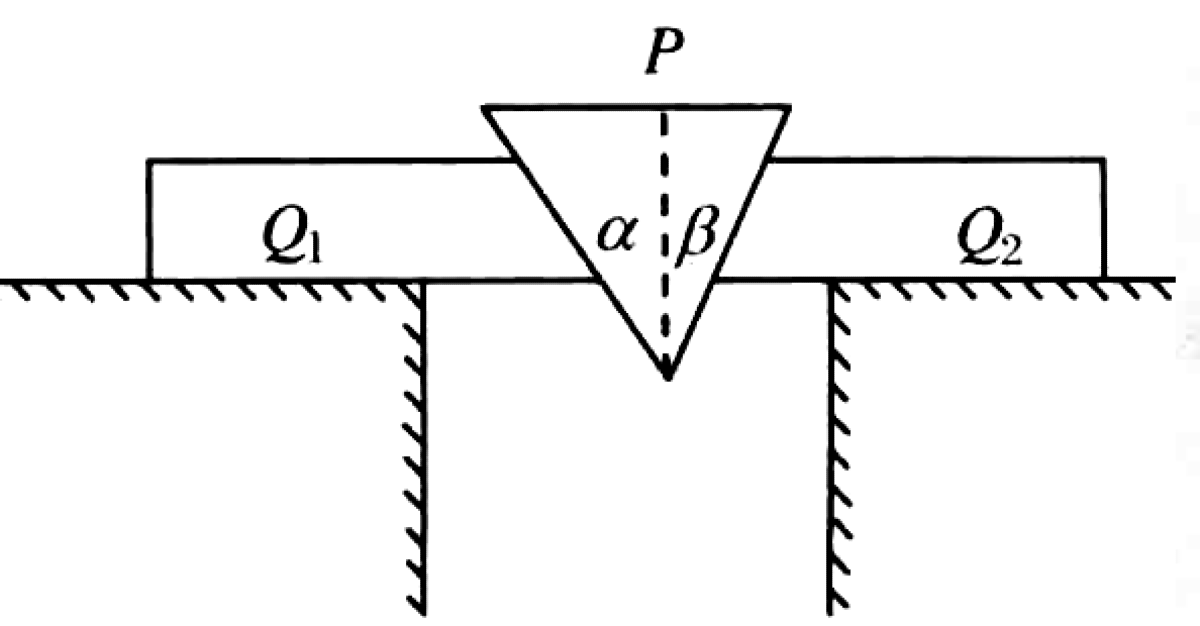
P0509-problem-1
The acceleration of block Q1 is:
$$a_1 = \frac{Mg(M\tan\alpha + m_2(\tan\alpha+\tan\beta))}{(M+m_1+m_2)^2 - (m_1\tan\alpha-m_2\tan\beta)(m_1\cot\alpha-m_2\cot\beta)}$$The acceleration of block Q2 is:
$$a_2 = \frac{Mg(M\tan\beta + m_1(\tan\alpha+\tan\beta))}{(M+m_1+m_2)^2 - (m_1\tan\alpha-m_2\tan\beta)(m_1\cot\alpha-m_2\cot\beta)}$$Let the downward vertical acceleration of wedge P be $a$ and its horizontal acceleration to the right be $a_x$. Let the acceleration of block Q1 to the left be $a_1$ and that of block Q2 to the right be $a_2$.
From the free-body diagrams and Newton's second law for each block: For block Q1 (horizontal): $N_1 \sin\alpha = m_1 a_1$ For block Q2 (horizontal): $N_2 \sin\beta = m_2 a_2$ For wedge P (horizontal): $N_1 \sin\alpha - N_2 \sin\beta = M a_x$ For wedge P (vertical): $Mg - N_1 \cos\alpha - N_2 \cos\beta = M a$
From the geometry of the system, the kinematic constraints relating the accelerations are found by ensuring the surfaces remain in contact. If P moves down by $dy$ and right by $dx$, Q1 moves left by $dx_1$ and Q2 moves right by $dx_2$.
$dx_1 = dy \tan\alpha - dx \implies a_1 = a \tan\alpha - a_x$ $dx_2 = dy \tan\beta + dx \implies a_2 = a \tan\beta + a_x$Substitute the force equations for Q1 and Q2 into the horizontal equation for P:
$$m_1 a_1 - m_2 a_2 = M a_x$$Substitute the kinematic constraints into this equation:
$$m_1(a \tan\alpha - a_x) - m_2(a \tan\beta + a_x) = M a_x$$ $$a(m_1 \tan\alpha - m_2 \tan\beta) = a_x(M + m_1 + m_2)$$Now use the vertical equation for P. First, substitute $N_1$ and $N_2$:
$$Mg - \frac{m_1 a_1}{\sin\alpha}\cos\alpha - \frac{m_2 a_2}{\sin\beta}\cos\beta = M a$$ $$Mg - m_1 a_1 \cot\alpha - m_2 a_2 \cot\beta = M a$$Substitute the kinematic constraints into this equation:
$$Mg - m_1(a \tan\alpha - a_x)\cot\alpha - m_2(a \tan\beta + a_x)\cot\beta = M a$$ $$Mg - m_1(a - a_x \cot\alpha) - m_2(a + a_x \cot\beta) = M a$$ $$Mg + a_x(m_1 \cot\alpha - m_2 \cot\beta) = a(M + m_1 + m_2)$$Let $S = M+m_1+m_2$, $T = m_1 \tan\alpha - m_2 \tan\beta$, and $C = m_1 \cot\alpha - m_2 \cot\beta$. The two equations for $a$ and $a_x$ are:
- $aT = a_x S$
- $Mg + a_x C = aS$
Solving this system, we find the vertical acceleration of the wedge P:
$$a = \frac{MgS}{S^2 - TC}$$And the horizontal acceleration of P:
$$a_x = \frac{MgT}{S^2 - TC}$$Finally, we find the accelerations of the blocks Q1 and Q2:
$$a_1 = a \tan\alpha - a_x = \frac{a}{S}(S \tan\alpha - T) = \frac{a}{S}(M\tan\alpha + m_2(\tan\alpha+\tan\beta))$$ $$a_2 = a \tan\beta + a_x = \frac{a}{S}(S \tan\beta + T) = \frac{a}{S}(M\tan\beta + m_1(\tan\alpha+\tan\beta))$$Substituting the expression for $a$:
$$a_1 = \frac{Mg(M\tan\alpha + m_2(\tan\alpha+\tan\beta))}{S^2 - TC}$$ $$a_2 = \frac{Mg(M\tan\beta + m_1(\tan\alpha+\tan\beta))}{S^2 - TC}$$The denominator is $S^2 - TC = (M+m_1+m_2)^2 - (m_1\tan\alpha-m_2\tan\beta)(m_1\cot\alpha-m_2\cot\beta)$.