Source: Physics Competition - Mechanics
Problem Sets:
Problem
As shown in the figure, the masses of the three objects A, B, and C are $m_A = \frac{2\sqrt{3}}{3}m$, $m_B = 2m$, and $m_C = m$, respectively. Object C is connected to sliders A and B by two ropes that pass over two light, smooth pulleys, $O_1$ and $O_2$, at the same height. Sliders A and B are on fixed, smooth inclined planes with angles 60° and 30°, respectively. The system is initially in equilibrium. An object D with mass $m_D=m$ is gently hung on a hook below object C.
- Find the acceleration of object A at the instant D is hung.
- Find the acceleration of object B at the instant D is hung.
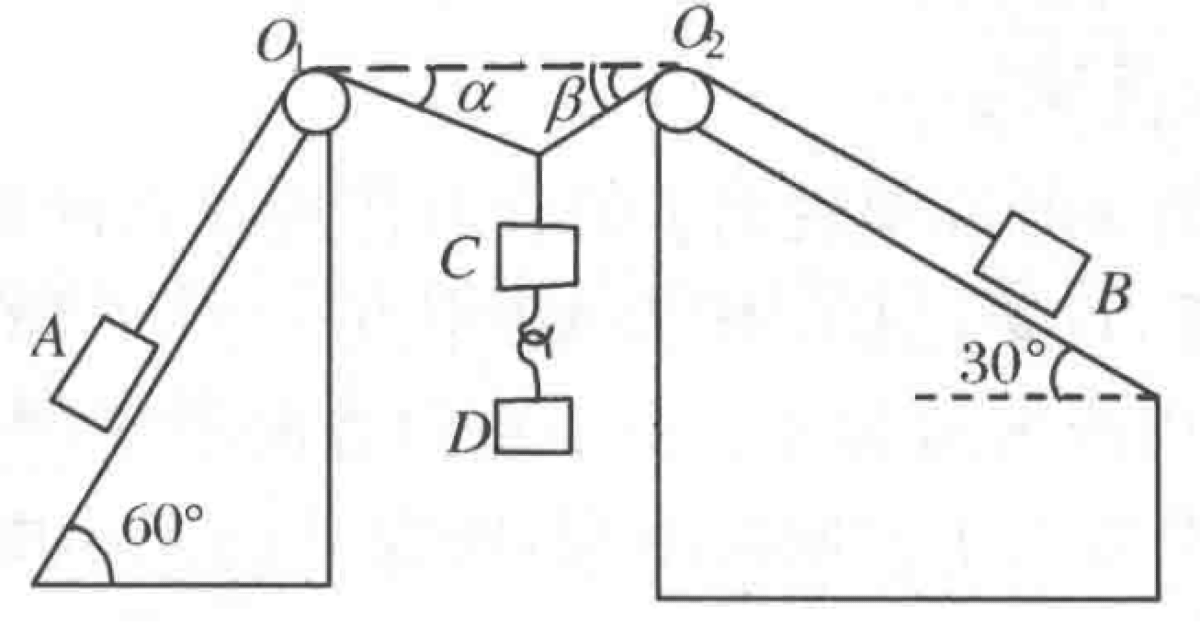
P0508-problem-1
Hints
Hint 1: Solve static problem first for $\alpha$ and $\beta$
Hint 2: Kinematic constraint at $t=0$: when all objects have zero velocity, the acceleration along the string is the same.
Hint 3: Because two objects on the slopes are not the same, the objects CD's acceleration is not vertical.
Hint 4: Write the dynamics equation for objects CD along the two rope direction, instead of $x$ and $y$
[Q1] The acceleration of object A is $$a_A = \frac{15g}{48 + 14\sqrt{3}} = \frac{15g}{2(24 + 7\sqrt{3})}$$ directed up the incline. [Q2] The acceleration of object B is $$a_B = \frac{3(2 + \sqrt{3})g}{48 + 14\sqrt{3}} = \frac{3(2 + \sqrt{3})g}{2(24 + 7\sqrt{3})}$$ directed up the incline.
Here is the corrected solution in the requested format.
1. Initial Equilibrium State
First, we analyze the system in equilibrium before object D is added. Let $T_A$ and $T_B$ be the rope tensions. For equilibrium of sliders A and B on the smooth inclines:
$$T_A = m_A g \sin(60°) = \left(\frac{2\sqrt{3}}{3}m\right) g \left(\frac{\sqrt{3}}{2}\right) = mg$$ $$T_B = m_B g \sin(30°) = (2m) g \left(\frac{1}{2}\right) = mg$$For the equilibrium of object C (mass $m_C = m$), let the ropes make angles $\alpha$ and $\beta$ with the horizontal line $O_1O_2$. Horizontal equilibrium: $T_A \cos \alpha = T_B \cos \beta$. Since $T_A = T_B$, we have $\alpha = \beta$. Vertical equilibrium: $T_A \sin \alpha + T_B \sin \beta = m_C g$.
$$2(mg) \sin \alpha = mg \implies \sin \alpha = \frac{1}{2} \implies \alpha = 30°$$Thus, in the initial equilibrium state, $\alpha = \beta = 30°$.
2. Kinematic Constraints at the Instant After D is Hung
At the instant D is hung, the geometry is unchanged ($\alpha = \beta = 30°$). We define the positive directions as:
- $a_A$: Acceleration of A **up** its incline.
- $a_B$: Acceleration of B **up** its incline.
- $\vec{a}_{CD} = a_x \hat{i} + a_y \hat{j}$: Acceleration of CD (positive $\hat{i}$ **right**, positive $\hat{j}$ **up**).
The unit vector from C towards pulley $O_1$ is $\hat{n}_A = (-\cos 30°, \sin 30°)$. The unit vector from C towards pulley $O_2$ is $\hat{n}_B = (\cos 30°, \sin 30°)$.
For A to accelerate up its incline (positive $a_A$), the rope segment $O_1C$ must lengthen. This means C must accelerate away from $O_1$. The acceleration of C relative to $O_1$ is $\vec{a}_{CD} \cdot (-\hat{n}_A)$.
$$a_A = \vec{a}_{CD} \cdot (-\hat{n}_A) = -( -a_x \cos 30° + a_y \sin 30° ) = a_x \cos 30° - a_y \sin 30°$$ $$a_B = \vec{a}_{CD} \cdot (-\hat{n}_B) = -( a_x \cos 30° + a_y \sin 30° ) = -a_x \cos 30° - a_y \sin 30°$$From these, we can express $a_x$ and $a_y$ in terms of $a_A$ and $a_B$:
$$a_A + a_B = -2 a_y \sin 30° = -a_y \implies a_y = -(a_A + a_B)$$ $$a_A - a_B = 2 a_x \cos 30° = \sqrt{3} a_x \implies a_x = \frac{a_A - a_B}{\sqrt{3}}$$3. Equations of Motion
Let $T'_A$ and $T'_B$ be the new tensions. The total mass hanging is $M_{CD} = m_C + m_D = 2m$. For object A (positive up the incline):
$$T'_A - m_A g \sin(60°) = m_A a_A \implies T'_A - mg = m_A a_A$$For object B (positive up the incline):
$$T'_B - m_B g \sin(30°) = m_B a_B \implies T'_B - mg = m_B a_B$$For the combined object CD: x-component: $T'_B \cos 30° - T'_A \cos 30° = M_{CD} a_x$ y-component: $T'_A \sin 30° + T'_B \sin 30° - M_{CD} g = M_{CD} a_y$
4. Solving for Accelerations
Substitute $T'_A = mg + m_A a_A$ and $T'_B = mg + m_B a_B$ into the equations for CD. From the x-equation for CD:
$$(T'_B - T'_A) \frac{\sqrt{3}}{2} = M_{CD} \left( \frac{a_A - a_B}{\sqrt{3}} \right)$$ $$( (mg+m_B a_B) - (mg+m_A a_A) ) \frac{\sqrt{3}}{2} = 2m \left( \frac{a_A - a_B}{\sqrt{3}} \right)$$ $$(m_B a_B - m_A a_A) \frac{3}{2} = 2m (a_A - a_B)$$ $$3(m_B a_B - m_A a_A) = 4m(a_A - a_B)$$Substituting $m_A = \frac{2\sqrt{3}}{3}m$ and $m_B = 2m$:
$$3\left(2m \cdot a_B - \frac{2\sqrt{3}}{3}m \cdot a_A\right) = 4m(a_A - a_B)$$ $$6 a_B - 2\sqrt{3} a_A = 4 a_A - 4 a_B$$ $$10 a_B = (4 + 2\sqrt{3}) a_A \implies 5 a_B = (2 + \sqrt{3}) a_A$$From the y-equation for CD:
$$(T'_A + T'_B) \frac{1}{2} - M_{CD} g = M_{CD} a_y$$Substitute $a_y = -(a_A + a_B)$:
$$( (mg+m_A a_A) + (mg+m_B a_B) ) \frac{1}{2} - 2mg = 2m(-(a_A + a_B))$$ $$mg + \frac{m_A}{2}a_A + \frac{m_B}{2}a_B - 2mg = -2m a_A - 2m a_B$$ $$-mg = -\left(2m + \frac{m_A}{2}\right) a_A - \left(2m + \frac{m_B}{2}\right) a_B$$ $$g = \left(2 + \frac{m_A}{2m}\right) a_A + \left(2 + \frac{m_B}{2m}\right) a_B$$ $$g = \left(2 + \frac{2\sqrt{3}/3}{2}\right) a_A + \left(2 + \frac{2}{2}\right) a_B$$ $$g = \left(2 + \frac{\sqrt{3}}{3}\right) a_A + 3 a_B = \left(\frac{6 + \sqrt{3}}{3}\right) a_A + 3 a_B$$We now solve the system:
- $a_B = \frac{2 + \sqrt{3}}{5} a_A$
- $g = \left(\frac{6 + \sqrt{3}}{3}\right) a_A + 3 a_B$
Substitute (1) into (2):
$$g = \left(\frac{6 + \sqrt{3}}{3}\right) a_A + 3 \left(\frac{2 + \sqrt{3}}{5}\right) a_A$$ $$g = \left[ \frac{5(6 + \sqrt{3}) + 9(2 + \sqrt{3})}{15} \right] a_A$$ $$g = \left[ \frac{30 + 5\sqrt{3} + 18 + 9\sqrt{3}}{15} \right] a_A$$ $$g = \left( \frac{48 + 14\sqrt{3}}{15} \right) a_A$$[Q1] Answer:
$$a_A = \frac{15g}{48 + 14\sqrt{3}} = \frac{15g}{2(24 + 7\sqrt{3})}$$[Q2] Answer:
$$a_B = \left(\frac{2 + \sqrt{3}}{5}\right) a_A = \left(\frac{2 + \sqrt{3}}{5}\right) \left( \frac{15g}{48 + 14\sqrt{3}} \right)$$ $$a_B = \frac{3(2 + \sqrt{3})g}{48 + 14\sqrt{3}} = \frac{3(2 + \sqrt{3})g}{2(24 + 7\sqrt{3})}$$