Source: Physics Competition - Mechanics
Problem Sets:
Problem
A curved section of railway track has a radius of curvature $r$. The distance between the two rails is $L$, as shown in the figure.
- When a train passes through this curve at a rated speed $v_0$, what should be the height difference $h$ between the outer and inner rails so that the rails experience no lateral thrust?
- When the train passes through the curve at a speed $v (v > v_0)$, to prevent it from overturning, what is the maximum possible height of its center of mass?
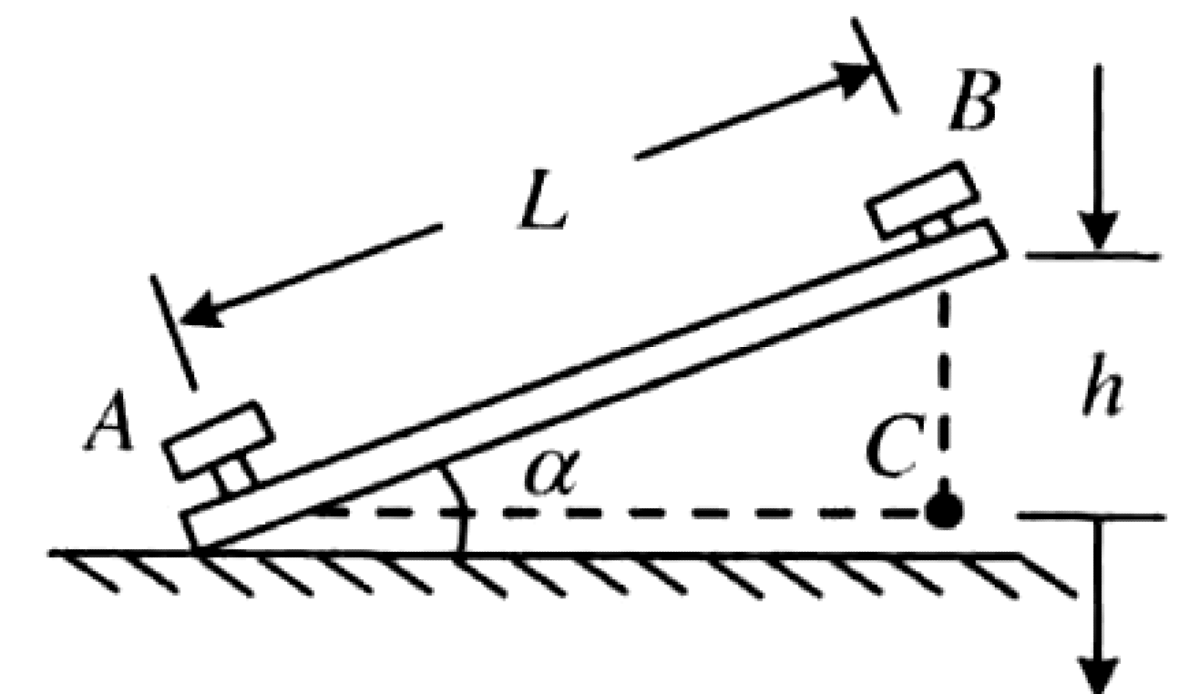
P0507-problem-1
[Q1] $h = \frac{L v_0^2}{gr}$ [Q2] $H_{max} = \frac{Lgr}{2(v^2-v_0^2)}\left(\frac{g r}{v_0^2} + \frac{v^2 v_0^2}{g^2 r^2} \right)$ or simplified as $H_{max} = \frac{L(g^2r^2 + v^2v_0^2)}{2gr(v^2-v_0^2)}$
Let the banking angle of the track be $\alpha$.
[Q1] For no lateral thrust, the centripetal force must be provided solely by the horizontal component of the total normal force $N$ from the rails. The vertical component of $N$ must balance the train's weight $mg$. Horizontal force:
$$N \sin\alpha = \frac{m v_0^2}{r}$$Vertical force:
$$N \cos\alpha = mg$$Dividing the two equations gives the ideal banking angle:
$$\tan\alpha = \frac{v_0^2}{gr}$$From the geometry of the track, the height difference is $h = L \sin\alpha$. For typical small banking angles, $\sin\alpha \approx \tan\alpha$.
$$h \approx L \tan\alpha = \frac{L v_0^2}{gr}$$[Q2] Overturning occurs when the train pivots about the outer rail (B), at which point the normal force from the inner rail (A) becomes zero. To analyze this, we balance the torques about the pivot point B in the train's non-inertial reference frame. Let $H$ be the height of the center of mass (CM) above the plane of the rails. The overturning torque is produced by the centrifugal force $F_c = m v^2/r$. The restoring torque is produced by gravity $mg$. At the tipping point, these torques are equal:
$$\tau_{\text{overturning}} = \tau_{\text{restoring}}$$ $$F_c (H \cos\alpha - \frac{L}{2} \sin\alpha) = mg (\frac{L}{2} \cos\alpha + H \sin\alpha)$$Substituting $F_c = m v^2/r$ and solving for the maximum height $H_{max}$:
$$H_{max} \left( \frac{v^2}{r} \cos\alpha - g \sin\alpha \right) = \frac{L}{2} \left( g \cos\alpha + \frac{v^2}{r} \sin\alpha \right)$$ $$H_{max} = \frac{L}{2} \frac{g \cos\alpha + (v^2/r) \sin\alpha}{g \sin\alpha - (v^2/r) \cos\alpha} = \frac{L}{2} \frac{g + (v^2/r)\tan\alpha}{g\tan\alpha - v^2/r}$$Substitute $\tan\alpha = v_0^2/(gr)$ from part 1:
$$H_{max} = \frac{L}{2} \frac{g + (v^2/r)(v_0^2/gr)}{g(v_0^2/gr) - v^2/r} = \frac{L(g^2r^2 + v^2v_0^2)}{2gr(v^2-v_0^2)}$$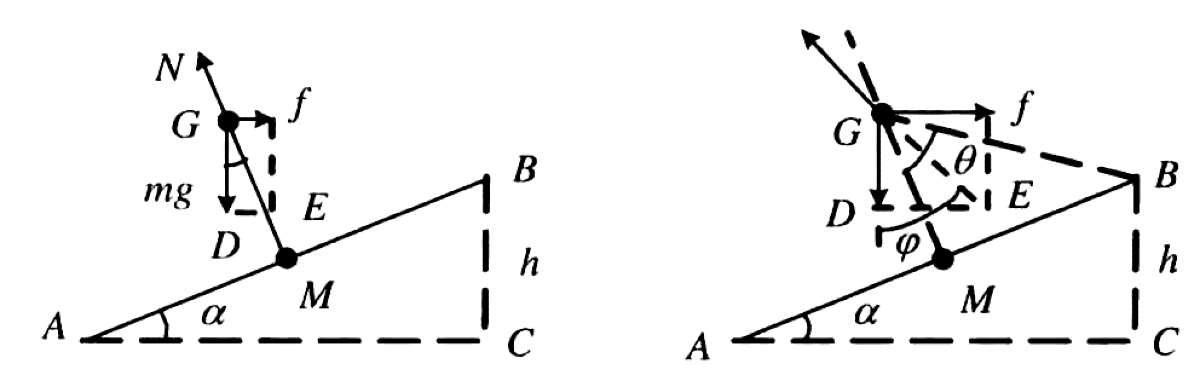
P0507-solution-1