P0506 Mechanics › Dynamics

Block Sliding Down a Frictionless Movable Wedge

← Back to Problems
Dynamics Advanced Incline Non-inertial reference center-of-mass

Source: Physics Competition - Mechanics

Problem Sets:

Work-energy-dynamics 1029

Problem

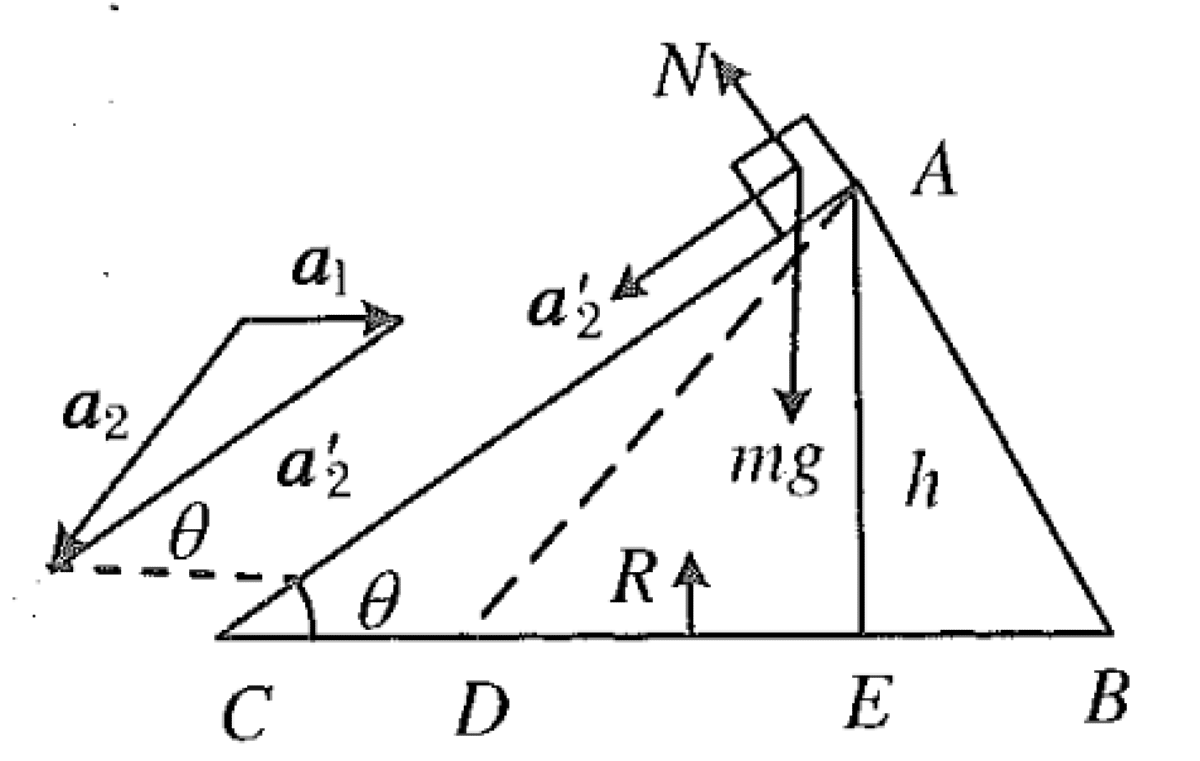
A wedge ABC of mass $M$ and height $h$ has an inclined surface AC with an angle $\theta$. A small object of mass $m$ is placed at the top A and slides down from rest. All contact surfaces are frictionless. Find:

  1. The displacement of $M$ when $m$ slides from the top to the bottom.
  2. The acceleration of $M$ relative to the ground, $a_1$, while $m$ is sliding.
  3. The acceleration of $m$ relative to $M$, $a'_2$.
  4. The acceleration of $m$ relative to the ground, $a_2$.
  5. The interaction force $N$ between $m$ and $M$.
  6. The normal force $R$ between $M$ and the table.

[Q1] Displacement of M: $\frac{m h \cot\theta}{M+m}$ [Q2] $a_1 = \frac{m g \sin\theta \cos\theta}{M + m\sin^2\theta}$ [Q3] $a'_2 = \frac{(M+m)g\sin\theta}{M+m\sin^2\theta}$ [Q4] $a_2 = \frac{g\sin\theta}{M+m\sin^2\theta}\sqrt{M^2\cos^2\theta + (M+m)^2\sin^2\theta}$ [Q5] $N = \frac{m M g \cos\theta}{M + m\sin^2\theta}$ [Q6] $R = \frac{M(M+m)g}{M+m\sin^2\theta}$

We use a ground-based coordinate system with x-axis horizontal to the right and y-axis vertical upwards. The wedge $M$ is pushed left; let its acceleration be $\vec{a}_1 = (-a_1, 0)$ where $a_1$ is the magnitude. The acceleration of the block $m$ is $\vec{a}_2 = (a_{2x}, a_{2y})$.

  1. Displacement of M (Q1): The system has no external horizontal forces, so the center of mass (CM) does not move horizontally. Let $x_M$ and $x_m$ be the horizontal displacements.

    $$M x_M + m x_m = 0$$

    The horizontal displacement of $m$ relative to $M$ is $d = h / \tan\theta = h\cot\theta$. So, the displacement of $m$ relative to the ground is $x_m = x_M + d$.

    $$M x_M + m (x_M + h\cot\theta) = 0 \implies (M+m)x_M = -m h\cot\theta$$

    The magnitude of the displacement of M is $|x_M| = \frac{m h \cot\theta}{M+m}$.

  2. Equations of Motion: Let $N$ be the normal force on $m$ from $M$. It acts perpendicular to the incline. For block $m$:

    $$N\sin\theta = m a_{2x} \quad (1)$$ $$N\cos\theta - mg = m a_{2y} \quad (2)$$

    For wedge $M$: The force from $m$ is $N$, directed down and left.

    $$-N\sin\theta = M(-a_1) \implies N\sin\theta = M a_1 \quad (3)$$ $$R - Mg - N\cos\theta = 0 \quad (4)$$

    Kinematic constraint: The acceleration of $m$ relative to $M$ is along the incline.

    $$\frac{a_{2y}}{a_{2x} - (-a_1)} = -\tan\theta \implies a_{2y}\cos\theta + (a_{2x}+a_1)\sin\theta = 0 \quad (5)$$

  3. Solving the System: Substitute $a_{2x}$, $a_{2y}$, and $a_1$ from (1), (2), (3) into (5):

    $$(\frac{N\cos\theta-mg}{m})\cos\theta + (\frac{N\sin\theta}{m})\sin\theta + (\frac{N\sin\theta}{M})\sin\theta = 0$$

    Solving for $N$ (Q5):

    $$N = \frac{m M g \cos\theta}{M + m\sin^2\theta}$$

    Using this result for the other quantities:

    • Acceleration of M (Q2):
    $$a_1 = \frac{N\sin\theta}{M} = \frac{m g \sin\theta \cos\theta}{M + m\sin^2\theta}$$
    • Acceleration of m relative to ground (Q4):
    $a_{2x} = \frac{N\sin\theta}{m} = \frac{M g \sin\theta \cos\theta}{M + m\sin^2\theta}$ $a_{2y} = \frac{N\cos\theta-mg}{m} = \frac{M g \cos^2\theta - g(M+m\sin^2\theta)}{M+m\sin^2\theta} = -\frac{(M+m)g\sin^2\theta}{M+m\sin^2\theta}$ $a_2 = \sqrt{a_{2x}^2 + a_{2y}^2} = \frac{g\sin\theta}{M+m\sin^2\theta}\sqrt{M^2\cos^2\theta + (M+m)^2\sin^2\theta}$
    • Acceleration of m relative to M (Q3): The relative acceleration $a'_2$ is along the incline. Its magnitude is:
    $$a'_2 = \frac{a_{2x}+a_1}{\cos\theta} = \frac{1}{\cos\theta}(\frac{N\sin\theta}{m} + \frac{N\sin\theta}{M}) = \frac{(M+m)g\sin\theta}{M+m\sin^2\theta}$$
    • Normal force from table (Q6):
    $$R = Mg + N\cos\theta = Mg + \frac{m M g \cos^2\theta}{M + m\sin^2\theta} = \frac{M(M+m)g}{M+m\sin^2\theta}$$
P0506-solution-1

P0506-solution-1