Source: Physics Competition - Mechanics
Problem
An inclined plane with side ratios 3:4:5 is fixed on a horizontal turntable. A wooden block is placed on the inclined plane and remains stationary at a distance $r = 40$ cm from the center of the turntable. The coefficient of static friction between the block and the plane is $\mu_s = 1/4$.
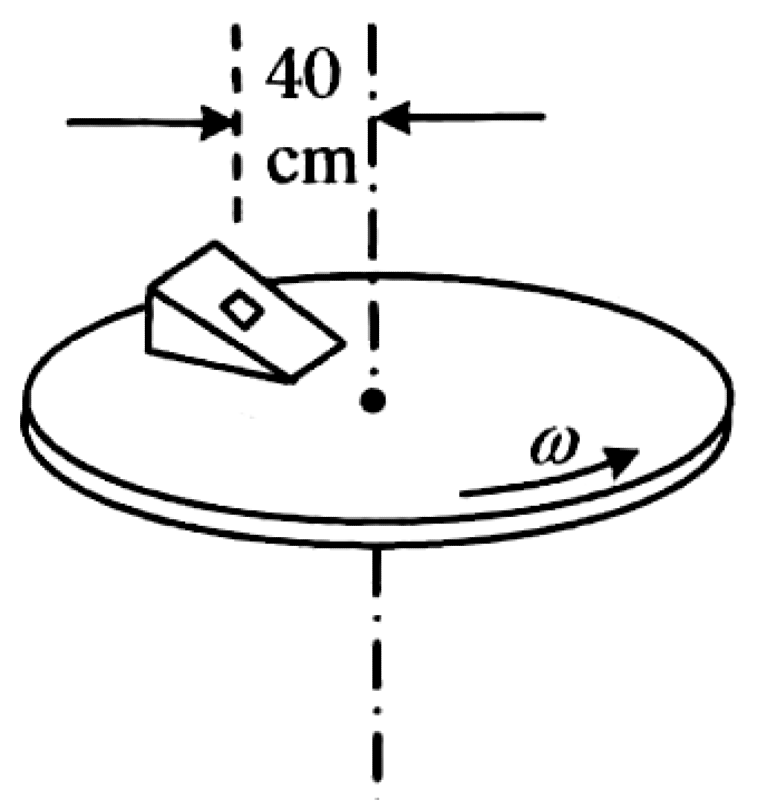
P0505-problem-1
Let $\theta$ be the angle of inclination. The 3:4:5 side ratios give $\sin\theta = 3/5$ and $\cos\theta = 4/5$. The forces acting on the block are gravity ($mg$), the normal force ($N$), and static friction ($f_s$). The net horizontal force provides the centripetal force $F_c = m\omega^2 r$.
For the minimum angular velocity, the block is on the verge of sliding down the incline. Therefore, the static friction force acts up the incline with its maximum value, $f_s = \mu_s N$.
We resolve the forces into horizontal (radial) and vertical components. Vertical equilibrium ($\sum F_y = 0$):
$$N\cos\theta + f_s\sin\theta - mg = 0$$Substituting $f_s = \mu_s N$:
$$N(\cos\theta + \mu_s\sin\theta) = mg \quad (1)$$Horizontal dynamics ($\sum F_x = m\omega^2 r$): The net force towards the center of rotation is the centripetal force.
$$N\sin\theta - f_s\cos\theta = m\omega^2 r$$Substituting $f_s = \mu_s N$:
$$N(\sin\theta - \mu_s\cos\theta) = m\omega^2 r \quad (2)$$Divide equation (2) by equation (1) to eliminate $N$ and $m$:
$$\frac{\sin\theta - \mu_s\cos\theta}{\cos\theta + \mu_s\sin\theta} = \frac{\omega^2 r}{g}$$Solving for $\omega$:
$$\omega = \sqrt{\frac{g}{r} \frac{\sin\theta - \mu_s\cos\theta}{\cos\theta + \mu_s\sin\theta}}$$Substitute the given values: $r = 0.4$ m, $\mu_s = 1/4$, $\sin\theta = 3/5$, $\cos\theta = 4/5$, and assuming $g = 9.8$ m/s$^2$.
$$\omega^2 = \frac{g}{0.4} \frac{3/5 - (1/4)(4/5)}{4/5 + (1/4)(3/5)} = \frac{g}{0.4} \frac{3/5 - 1/5}{4/5 + 3/20} = \frac{g}{0.4} \frac{2/5}{19/20} = \frac{g}{0.4} \frac{8}{19}$$ $$\omega^2 = \frac{2.5g \cdot 8}{19} = \frac{20g}{19} = \frac{20(9.8)}{19} = \frac{196}{19}$$ $$\omega = \sqrt{\frac{196}{19}} = \frac{14}{\sqrt{19}} \text{ rad/s}$$