Source: Physics Competition - Mechanics
Problem
A double pendulum system consists of two inextensible light strings of lengths $l_1$ and $l_2$, and two small balls A and B with masses $m_1$ and $m_2$ respectively. Ball A is is connected with string $l_1$ from the ceiling, and ball B is at the bottom, connected to ball A via string $l_2$. The system is initially in a vertical equilibrium position. A third ball C, also with mass $m_1$, collides elastically with ball A at a horizontal velocity $v_0$.
- Find the tension $T_1$ in the upper string immediately after the collision.
- Find the tension $T_2$ in the lower string immediately after the collision.
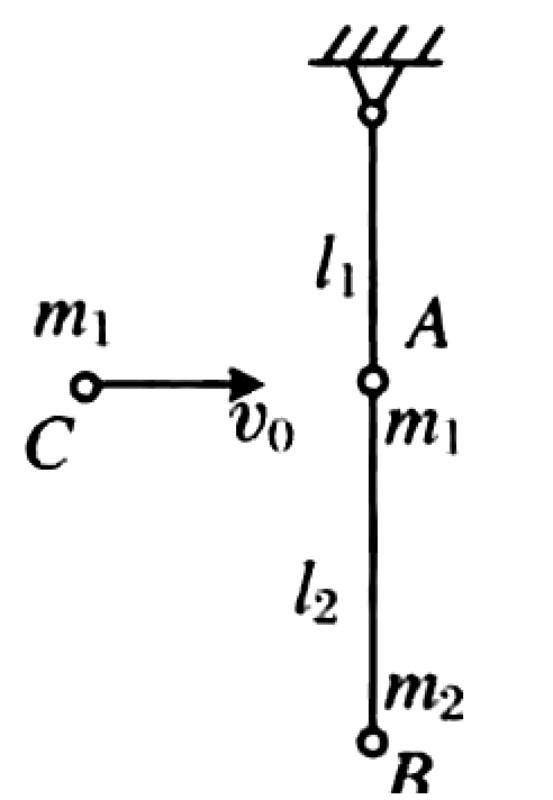
P0503-problem-1
The tension in the upper string immediately after the collision is:
$$T_1 = (m_1 + m_2)g + v_0^2 \left(\frac{m_1 + m_2}{l_1} + \frac{m_2}{l_2}\right)$$The tension in the lower string immediately after the collision is:
$$T_2 = m_2 g + m_2 v_0^2 \left(\frac{1}{l_1} + \frac{1}{l_2}\right)$$Here is the solution based on the provided format.
The analysis is performed immediately after the collision, at which point the strings are still vertical. Let the upward direction be positive.
1. State Immediately After Collision The collision is elastic between ball C (mass $m_1$) and ball A (mass $m_1$), with A initially at rest. For such a collision, the velocities are exchanged.
- Ball A acquires the velocity of ball C: $v_A = v_0$ (horizontal).
- Ball C comes to rest.
The collision is instantaneous. The finite tension forces in the strings provide no impulse, so the velocity of ball B remains zero.
- Velocity of ball B: $v_B = 0$.
2. Kinematics of Accelerations Immediately after the collision, we determine the vertical accelerations $a_{Ay}$ and $a_{By}$ for balls A and B, respectively.
- Ball A begins to move in a circular path of radius $l_1$. Its velocity is purely horizontal ($v_A=v_0$). The centripetal acceleration is directed vertically upwards towards the pivot.
- To find the acceleration of B, we consider its motion relative to A. The relative velocity is $\vec{v}_{B/A} = \vec{v}_B - \vec{v}_A = 0 - v_0\hat{i} = -v_0\hat{i}$. Ball B starts to move in a circle of radius $l_2$ relative to A. The centripetal acceleration of B relative to A is directed from B towards A (upwards).
- The absolute acceleration of B is the sum of the acceleration of A and the relative acceleration of B with respect to A ($\vec{a}_B = \vec{a}_A + \vec{a}_{B/A}$). For the vertical components:
3. Dynamics and Tensions We apply Newton's second law in the vertical direction to each ball.
[Q2] Tension $T_2$ in the lower string Consider the free-body diagram for ball B ($m_2$). The net vertical force is $T_2 - m_2 g$.
$$T_2 - m_2 g = m_2 a_{By}$$ $$T_2 = m_2 g + m_2 a_{By} = m_2 g + m_2 v_0^2 \left(\frac{1}{l_1} + \frac{1}{l_2}\right)$$[Q1] Tension $T_1$ in the upper string Consider the free-body diagram for ball A ($m_1$). The net vertical force is $T_1 - T_2 - m_1 g$.
$$T_1 - T_2 - m_1 g = m_1 a_{Ay}$$ $$T_1 = T_2 + m_1 g + m_1 a_{Ay}$$Substituting the expressions for $T_2$ and $a_{Ay}$:
$$T_1 = \left[m_2 g + m_2 v_0^2 \left(\frac{1}{l_1} + \frac{1}{l_2}\right)\right] + m_1 g + m_1 \frac{v_0^2}{l_1}$$Grouping terms:
$$T_1 = (m_1 + m_2)g + v_0^2 \left(\frac{m_1}{l_1} + \frac{m_2}{l_1} + \frac{m_2}{l_2}\right)$$ $$T_1 = (m_1 + m_2)g + v_0^2 \left(\frac{m_1 + m_2}{l_1} + \frac{m_2}{l_2}\right)$$