Source: Physics Competition - Mechanics
Problem
A uniform rubber band of mass $m$, natural radius $r_1$, and stiffness coefficient $k$ is placed horizontally on a vertical cylinder of radius $r_2$ ($r_2 > r_1$). The mass distribution of the band remains uniform. The coefficient of static friction between the band and the cylinder is $\mu$. The cylinder rotates about its vertical axis with angular velocity $\omega$.
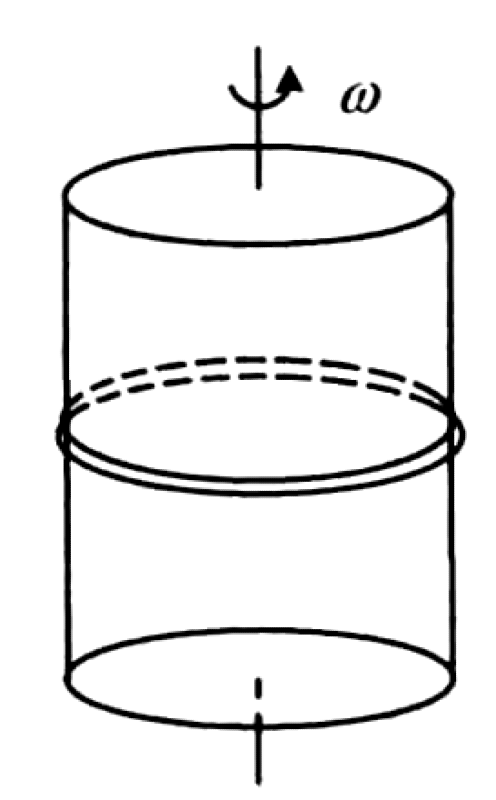
P0502-problem-1
First, we find the tension $T$ in the stretched rubber band. The extension of the circumference is $\Delta L = 2\pi r_2 - 2\pi r_1$. Using the stiffness coefficient $k$:
$$T = k \Delta L = 2\pi k(r_2-r_1)$$Next, we find the total normal force $N$ exerted by the cylinder on the band. Consider a small segment of the band. The net inward radial force on the segment (resultant of tension minus the outward normal force) provides the centripetal force required for rotation. Summing over the entire band gives the total normal force:
$$N = 2\pi T - m\omega^2 r_2$$For the band to remain in vertical equilibrium, the upward static friction force $f_s$ must balance the downward gravitational force $mg$. At the point of slipping, the required static friction equals the maximum available static friction:
$$mg = f_{s,max} = \mu N$$As the angular velocity $\omega$ increases, the normal force $N$ decreases, reducing the maximum static friction. The maximum angular velocity $\omega_{max}$ occurs when the friction is just sufficient to support the weight.
$$mg = \mu (2\pi T - m\omega_{max}^2 r_2)$$Substitute the expression for tension $T$:
$$mg = \mu (2\pi [2\pi k(r_2-r_1)] - m\omega_{max}^2 r_2)$$ $$mg = \mu (4\pi^2 k(r_2-r_1) - m\omega_{max}^2 r_2)$$Now, we solve for $\omega_{max}$:
$$m\omega_{max}^2 r_2 = 4\pi^2 k(r_2-r_1) - \frac{mg}{\mu}$$ $$\omega_{max}^2 = \frac{4\pi^2 k(r_2-r_1)}{mr_2} - \frac{g}{\mu r_2}$$