P0500 Mechanics › Dynamics

Dynamics of a Three-Block System with Friction

← Back to Problems
Dynamics Advanced Friction

Source: Physics Competition - Mechanics

Problem

Three blocks are stacked on a horizontal table. From top to bottom, their masses are $m_1 = 5m$, $m_2 = 3m$, and $m_3 = m$. A horizontal force $F$ is applied to the middle block, $m_2$. The coefficient of friction between block 1 and 2 is $4\mu$; between block 2 and 3 is $2\mu$; and between block 3 and the table is $\mu$. Assume the coefficients of static and kinetic friction are equal.

  1. Determine the acceleration of each block as a function of the applied force $F$.
  2. Determine the magnitude of each friction force ($f_{12}$ between 1 and 2, $f_{23}$ between 2 and 3, and $f_{3T}$ between 3 and the table) as a function of the applied force $F$.

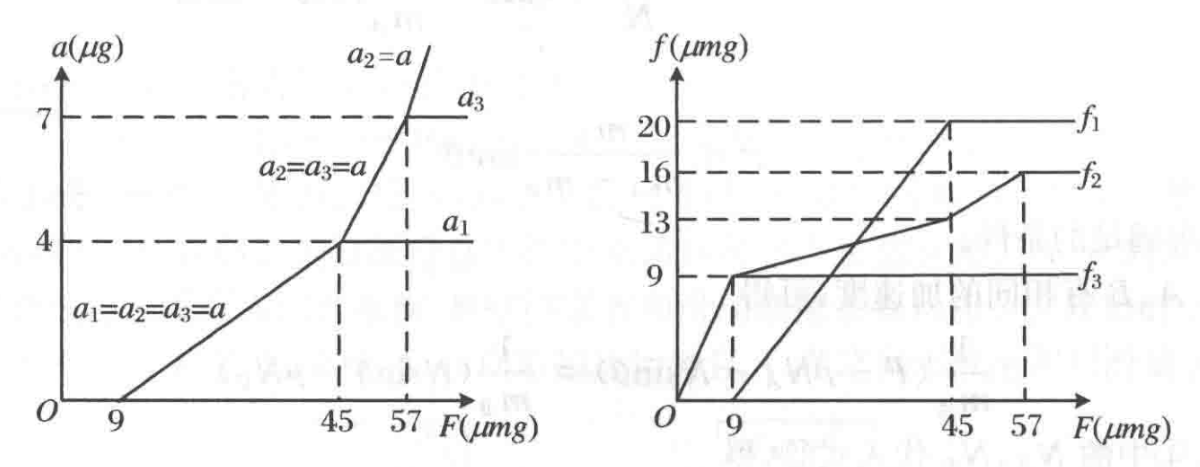
Let $F_0 = \mu mg$. The behavior is described in four regimes:

Regime 1: $0 \le F \le 9F_0$ Accelerations: $a_1 = a_2 = a_3 = 0$ Friction forces: $f_{12} = 0$, $f_{23} = F$, $f_{3T} = F$

Regime 2: $9F_0 < F \le 45F_0$ Accelerations: $a_1 = a_2 = a_3 = \frac{F - 9F_0}{9m}$ Friction forces: $f_{12} = \frac{5}{9}(F - 9F_0)$, $f_{23} = 8F_0 + \frac{F}{9}$, $f_{3T} = 9F_0$

Regime 3: $45F_0 < F \le 57F_0$ Accelerations: $a_1 = 4\mu g$, $a_2 = a_3 = \frac{F - 29F_0}{4m}$ Friction forces: $f_{12} = 20F_0$, $f_{23} = \frac{7F_0 + F}{4}$, $f_{3T} = 9F_0$

Regime 4: $F > 57F_0$ Accelerations: $a_1 = 4\mu g$, $a_2 = \frac{F - 36F_0}{3m}$, $a_3 = 7\mu g$ Friction forces: $f_{12} = 20F_0$, $f_{23} = 16F_0$, $f_{3T} = 9F_0$

First, calculate the maximum possible friction forces at each interface. The normal forces are $N_{12}=m_1g$, $N_{23}=(m_1+m_2)g$, and $N_{3T}=(m_1+m_2+m_3)g$.

$f_{12,max} = (4\mu)N_{12} = 4\mu(5m)g = 20\mu mg$ $f_{23,max} = (2\mu)N_{23} = 2\mu(5m+3m)g = 16\mu mg$ $f_{3T,max} = (\mu)N_{3T} = \mu(5m+3m+m)g = 9\mu mg$

The motion is analyzed in regimes based on which surfaces are slipping. Let $F_0 = \mu mg$.

  1. Static Regime ($0 \le F \le 9F_0$): The force $F$ is less than the maximum static friction with the table, $f_{3T,max}$. The entire system remains at rest.

    $a_1=a_2=a_3=0$.

    From FBDs: $f_{12}=0$, $f_{23}=F$, $f_{3T}=F$.

  2. All Blocks Move Together ($9F_0 < F \le 45F_0$): The system slides on the table with a common acceleration $a$. The total mass is $M = 9m$.

    $$F - f_{3T,max} = Ma \implies a = \frac{F - 9F_0}{9m}$$

    This holds as long as internal static frictions are not exceeded. Block 1: $f_{12} = m_1 a = 5m \left(\frac{F - 9F_0}{9m}\right) = \frac{5}{9}(F - 9F_0)$. Slipping occurs when $f_{12} = f_{12,max} \implies \frac{5}{9}(F - 9F_0) = 20F_0 \implies F = 45F_0$. Block 3: $f_{23} - f_{3T,max} = m_3 a \implies f_{23} = 9F_0 + m \left(\frac{F - 9F_0}{9m}\right) = 8F_0 + \frac{F}{9}$. Slipping occurs when $f_{23} = f_{23,max} \implies 8F_0 + \frac{F}{9} = 16F_0 \implies F = 72F_0$. The first slip occurs between blocks 1 and 2 when $F = 45F_0$.

  3. Block 1 Slips ($45F_0 < F \le 57F_0$): Block 1 moves with constant acceleration, as $f_{12}$ is now kinetic friction ($f_{12}=f_{12,max}$).

    $$a_1 = \frac{f_{12,max}}{m_1} = \frac{20F_0}{5m} = 4\mu g$$

    Blocks 2 and 3 move together with acceleration $a_{23}$.

    $$F - f_{12,max} - f_{3T,max} = (m_2+m_3)a_{23} \implies a_{23} = \frac{F - 20F_0 - 9F_0}{4m} = \frac{F - 29F_0}{4m}$$

    This holds as long as blocks 2 and 3 do not slip. Block 3: $f_{23} - f_{3T,max} = m_3 a_{23} \implies f_{23} = 9F_0 + m\left(\frac{F-29F_0}{4m}\right) = \frac{7F_0+F}{4}$. Slipping occurs when $f_{23} = f_{23,max} \implies \frac{7F_0+F}{4} = 16F_0 \implies F = 57F_0$.

  4. All Blocks Slip ($F > 57F_0$): All friction forces are at their maximum kinetic values. Block 1: $a_1 = 4\mu g$ (as before). Block 3: $f_{23,max} - f_{3T,max} = m_3 a_3 \implies 16F_0 - 9F_0 = m a_3 \implies a_3 = \frac{7F_0}{m} = 7\mu g$. Block 2: $F - f_{12,max} - f_{23,max} = m_2 a_2 \implies F - 20F_0 - 16F_0 = 3m a_2 \implies a_2 = \frac{F - 36F_0}{3m}$.

P0500-solution-1

P0500-solution-1