Source: Physics Competition - Mechanics
Problem Sets:
Problem
Two blocks A and B, with masses $m_A$ and $m_B$, are placed together on a horizontal table as shown in Figure (a). The contact surface between them is smooth and inclined at an angle $\theta$ to the horizontal. The coefficient of static and kinetic friction between each block and the table is $\mu$. A horizontal force F is applied to block A.
- Find the acceleration $a$ of the system in terms of $F$ and other given parameters.
- Find the range of the applied force $F$ for which both blocks accelerate to the right together without relative slipping.
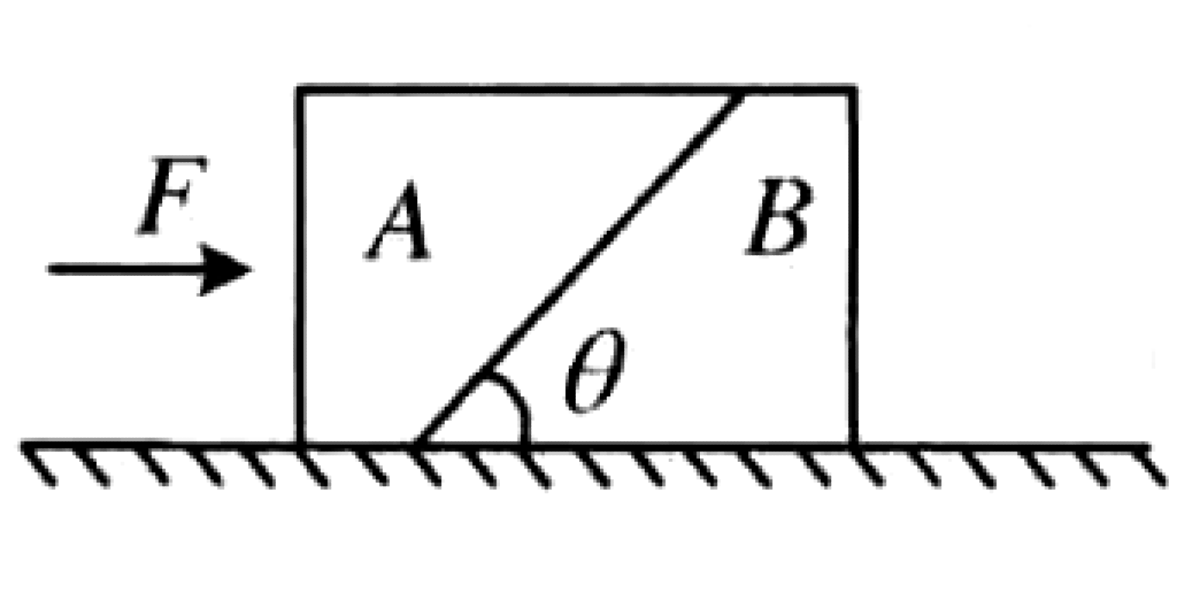
P0499-problem-1
[Q1] $a = \frac{F}{m_A + m_B} - \mu g$ [Q2] $\mu(m_A+m_B)g < F \le (m_A+m_B)g(\mu+\tan\theta)$
Let the system of two blocks have a total mass $M = m_A + m_B$. The system accelerates horizontally with acceleration $a$. The total kinetic friction force is $f_k = \mu N_{total} = \mu Mg = \mu(m_A+m_B)g$. Applying Newton's second law to the entire system:
$$F - f_k = Ma \implies F - \mu(m_A+m_B)g = (m_A+m_B)a$$The acceleration of the system is:
$$a = \frac{F}{m_A + m_B} - \mu g$$For the blocks to move together without relative slipping, block B must not lift off the table. Let $N$ be the normal force between A and B, and $N_B$ be the normal force from the table on B. Analyzing forces on block B: Vertical equilibrium: $N_B + N\cos\theta - m_B g = 0$ Horizontal motion: $N\sin\theta - \mu N_B = m_B a$
From the vertical equation, $N_B = m_B g - N\cos\theta$. The condition that B does not lift off is $N_B \ge 0$, which implies $N\cos\theta \le m_B g$. Substitute $N_B$ into the horizontal equation to find $N$:
$N\sin\theta - \mu(m_B g - N\cos\theta) = m_B a \implies N = \frac{m_B(a+\mu g)}{\sin\theta+\mu\cos\theta}$Now apply the no-lift condition:
$$\frac{m_B(a+\mu g)}{\sin\theta+\mu\cos\theta}\cos\theta \le m_B g$$ $$(a+\mu g)\cos\theta \le g(\sin\theta+\mu\cos\theta) \implies a\cos\theta \le g\sin\theta$$ $$a \le g\tan\theta$$For the system to accelerate, we need $a>0$. Combining conditions: $0 < a \le g\tan\theta$. In terms of force $F$: Lower bound: $a > 0 \implies \frac{F}{m_A + m_B} - \mu g > 0 \implies F > \mu(m_A+m_B)g$. Upper bound: $a \le g\tan\theta \implies \frac{F}{m_A + m_B} - \mu g \le g\tan\theta \implies F \le (m_A+m_B)g(\mu+\tan\theta)$.