Source: Physics Competition - Mechanics
Problem Sets:
Problem
As shown in the figure, for an ellipse with semi-major axis $a$ and semi-minor axis $b$, assume the major axis is vertical. A point mass of mass $m$ slides without friction under gravity along various straight chords passing through the center of the ellipse (referred to as "diameters").
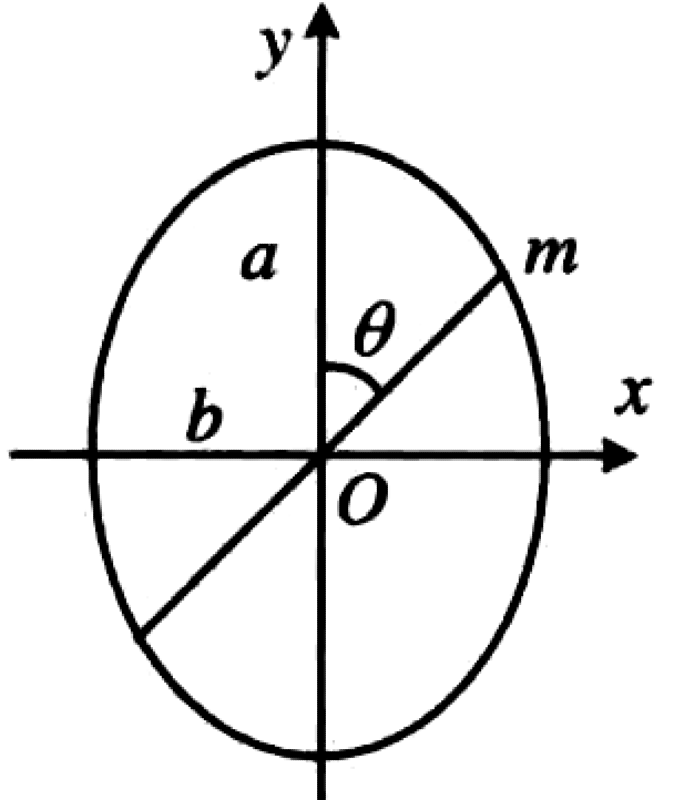
P0498-problem-1
The chord for the shortest sliding time depends on the ratio of the semi-axes $a$ and $b$:
- If $a < \sqrt{2}b$, the shortest time is along the vertical major axis ($\theta=0$).
- If $a \ge \sqrt{2}b$, the shortest time is along the chord making an angle $\theta$ with the vertical, where $\cos\theta = \frac{a}{\sqrt{2(a^2-b^2)}}$.
Let a chord through the center make an angle $\theta$ with the vertical y-axis. The point mass slides from the upper endpoint of the chord to the lower endpoint.
The length of the chord is $L = 2r$, where $r$ is the radial distance from the center to the ellipse. The component of gravitational acceleration along the chord is $a_{slide} = g \cos\theta$. The time $t$ to slide the length $L$ from rest is given by the kinematic equation $L = \frac{1}{2} a_{slide} t^2$.
$$t^2 = \frac{2L}{a_{slide}} = \frac{4r}{g \cos\theta}$$To find the shortest time, we need to minimize $t^2$.
The equation of the ellipse with the semi-major axis $a$ along the y-axis and semi-minor axis $b$ along the x-axis is $(\frac{x}{b})^2 + (\frac{y}{a})^2 = 1$. In polar coordinates, with $\theta$ measured from the y-axis, we have $x = r \sin\theta$ and $y = r \cos\theta$. Substituting these into the ellipse equation gives the radial distance $r$:
$$r^2 \left( \frac{\sin^2\theta}{b^2} + \frac{\cos^2\theta}{a^2} \right) = 1 \implies r = \frac{ab}{\sqrt{a^2 \sin^2\theta + b^2 \cos^2\theta}}$$Substituting $r$ into the equation for $t^2$:
$$t^2 = \frac{4ab}{g} \frac{1}{\cos\theta \sqrt{a^2 \sin^2\theta + b^2 \cos^2\theta}}$$Minimizing $t^2$ is equivalent to maximizing the denominator function $F(\theta) = (\cos\theta \sqrt{a^2 \sin^2\theta + b^2 \cos^2\theta})^2$.
$$F(\theta) = \cos^2\theta (a^2(1-\cos^2\theta) + b^2 \cos^2\theta)$$Let $u = \cos^2\theta$, where $u \in [0, 1]$. The function to maximize is:
$$G(u) = u(a^2(1-u) + b^2 u) = a^2 u - (a^2 - b^2)u^2$$This is a downward-opening parabola. Its vertex is at $u = \frac{-a^2}{2(-(a^2-b^2))} = \frac{a^2}{2(a^2-b^2)}$.
Two cases must be considered:
-
If the vertex is within the valid range, i.e., $\frac{a^2}{2(a^2-b^2)} \le 1$, which simplifies to $a \ge \sqrt{2}b$. The maximum of $G(u)$ occurs at the vertex. The shortest time is for the chord where $\cos^2\theta = \frac{a^2}{2(a^2-b^2)}$.
-
If the vertex is outside the valid range, i.e., $\frac{a^2}{2(a^2-b^2)} > 1$, which simplifies to $a < \sqrt{2}b$. The function $G(u)$ is monotonically increasing on the interval $[0, 1]$. The maximum occurs at the boundary $u=1$. The shortest time is for the chord where $\cos^2\theta = 1$, which means $\theta=0$ (the vertical major axis).