Source: Physics Competition - Mechanics
Problem
As shown in the figure, a block of mass $m$ is placed on the smooth inclined surface of a wedge. It is held in place by a thin string, with the other end of the string attached to a fixed backstop at the top of the wedge. Assume the angle of inclination is $\theta = 30^\circ$. The string will break when its tension reaches $2mg$. The entire system accelerates to the right with acceleration $a$.
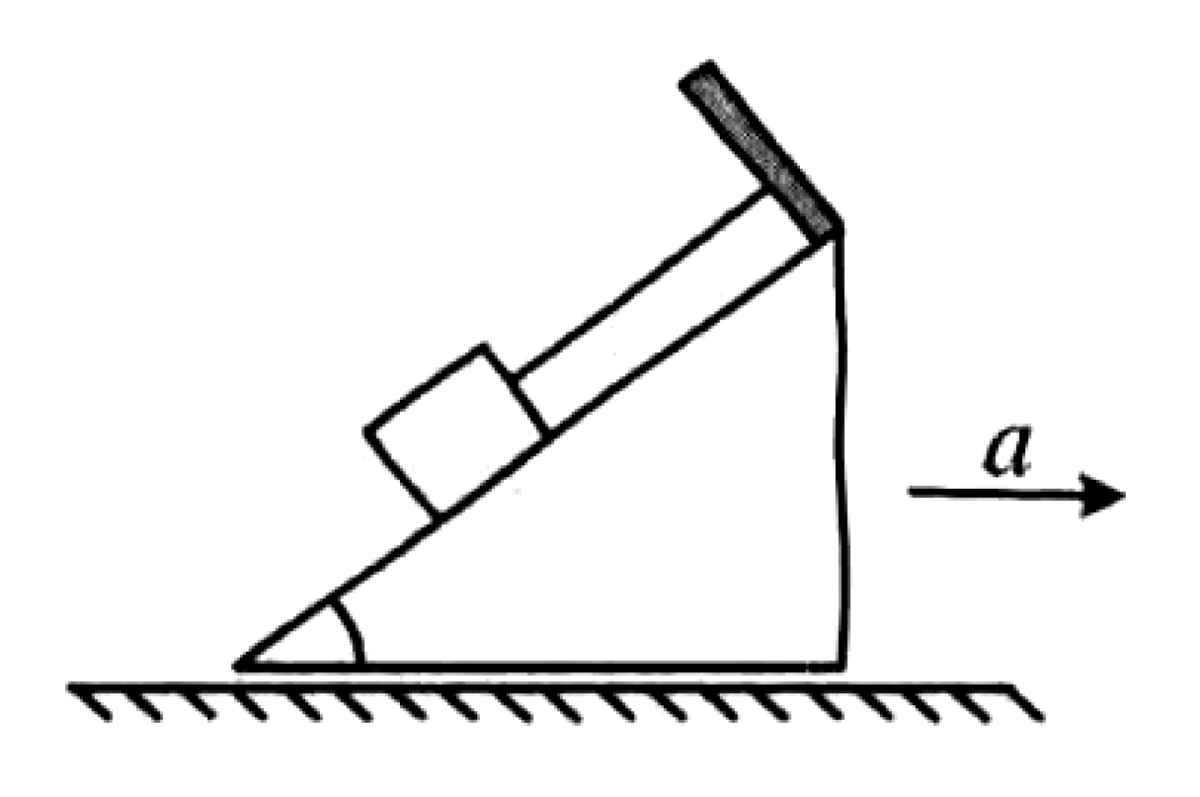
P0497-problem-1
We analyze the forces on the block $m$ in an inertial reference frame (the ground). The forces are gravity $mg$, the normal force $F_N$ from the wedge, and the tension $T$ from the string. The block's acceleration is $a$ horizontally.
Let's use a standard coordinate system with x horizontal and y vertical. We apply Newton's second law, $\Sigma \vec{F} = m\vec{a}$.
In the x-direction:
$$T\cos\theta - F_N\sin\theta = ma$$In the y-direction:
$$T\sin\theta + F_N\cos\theta - mg = 0$$We solve this system of two linear equations for $T$ and $F_N$. Multiplying the first equation by $\cos\theta$ and the second by $\sin\theta$ and adding them gives an expression for $T$:
$$(T\cos^2\theta - F_N\sin\theta\cos\theta) + (T\sin^2\theta + F_N\cos\theta\sin\theta) = ma\cos\theta + mg\sin\theta$$ $$T(\cos^2\theta + \sin^2\theta) = m(a\cos\theta + g\sin\theta) \implies T = m(a\cos\theta + g\sin\theta)$$Solving for $F_N$ from the y-direction equation: $F_N = \frac{mg - T\sin\theta}{\cos\theta}$. Substituting the expression for $T$:
$$F_N = \frac{mg - m(a\cos\theta + g\sin\theta)\sin\theta}{\cos\theta} = \frac{m(g - a\sin\theta\cos\theta - g\sin^2\theta)}{\cos\theta}$$ $$F_N = \frac{m(g(1-\sin^2\theta) - a\sin\theta\cos\theta)}{\cos\theta} = \frac{m(g\cos^2\theta - a\sin\theta\cos\theta)}{\cos\theta}$$ $$F_N = m(g\cos\theta - a\sin\theta)$$For the block to remain on the wedge, two conditions must be met:
- The string does not break: $T \le 2mg$
- The block does not lose contact with the wedge: $F_N \ge 0$
The maximum acceleration $a_{max}$ is the smaller of these two limits. Given $\theta=30^\circ$, $\sin\theta = 1/2$, $\cos\theta = \sqrt{3}/2$. From condition 1:
$$a \le g \frac{2 - 1/2}{\sqrt{3}/2} = g \frac{3/2}{\sqrt{3}/2} = \frac{3}{\sqrt{3}}g = \sqrt{3}g$$From condition 2:
$$a \le g\cot(30^\circ) = \sqrt{3}g$$Both conditions give the same limit, so the maximum acceleration is $\sqrt{3}g$.