Source: Physics Competition - Mechanics
Problem
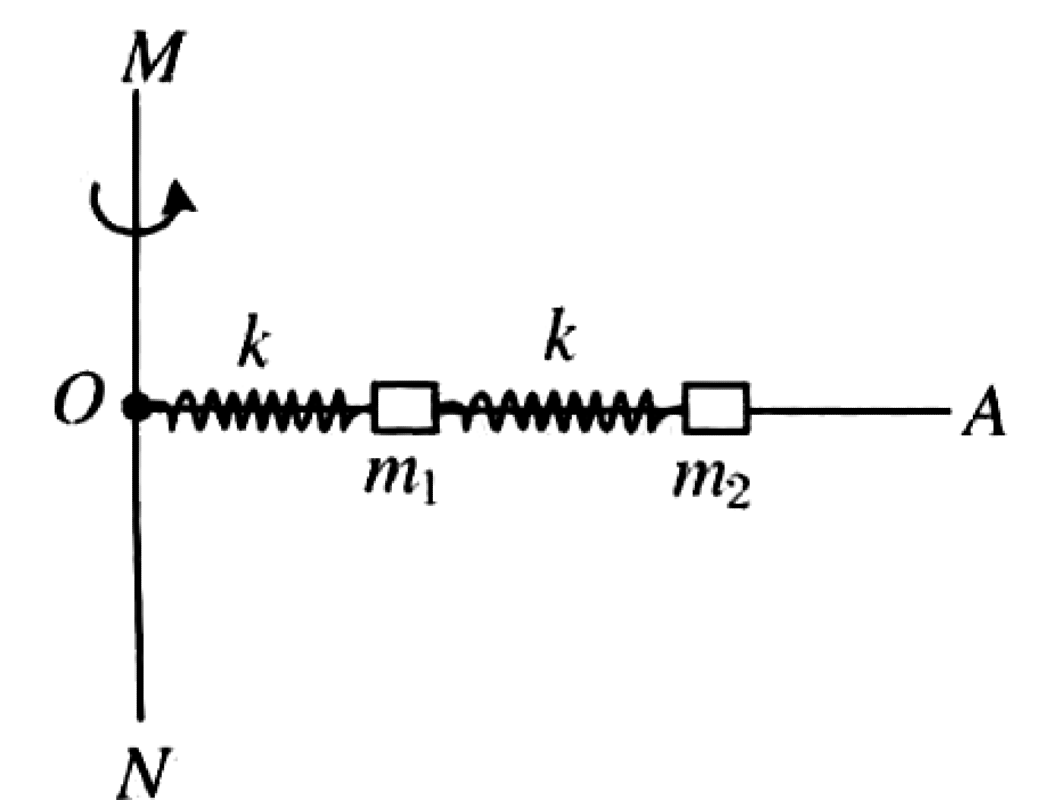
A smooth, thin horizontal rod OA can rotate about a vertical axis MN passing through O. Two identical small objects, each with mass $m_1 = m_2 = m$, are threaded onto the rod. They are connected by two identical light springs, each with spring constant $k$ and natural length $L_0$. The first spring connects the axis at O to mass $m_1$, and the second spring connects mass $m_1$ to mass $m_2$.
P0496-problem-1
Let $r_1$ and $r_2$ be the distances of masses $m_1$ and $m_2$ from the axis of rotation O. For a stable, steady rotation, the net force on each mass must provide the required centripetal force. Let the natural length of each spring be $L_0$.
For the outer mass $m_2$, the net force is from the second spring:
$$F_2 = k(r_2 - r_1 - L_0) = m\omega^2 r_2 \quad (1)$$For the inner mass $m_1$, the net force is the difference between the forces from the two springs:
$$F_1 - F_2 = k(r_1 - L_0) - k(r_2 - r_1 - L_0) = m\omega^2 r_1 \quad (2)$$This is a system of two linear equations for $r_1$ and $r_2$. We can solve for $r_1$ and $r_2$ in terms of $\omega$:
$$r_1 = \frac{L_0 k^2}{m^2\omega^4 - 3km\omega^2 + k^2}$$ $$r_2 = \frac{L_0 k(2k - m\omega^2)}{m^2\omega^4 - 3km\omega^2 + k^2}$$For a physically meaningful stable solution, the radii $r_1$ and $r_2$ must be positive, and the springs must be under tension (stretched). The condition of positive spring elongation ($r_1 > L_0$ and $r_2 - r_1 > L_0$) is guaranteed if $r_1$ and $r_2$ are positive. Let the denominator be $D(\omega^2) = m^2\omega^4 - 3km\omega^2 + k^2$.
The condition $r_1 > 0$ requires $D(\omega^2) > 0$. The roots of $D(\omega^2) = 0$ for $\omega^2$ are:
$$\omega^2 = \frac{3km \pm \sqrt{9k^2m^2 - 4m^2k^2}}{2m^2} = \frac{k}{m} \frac{3 \pm \sqrt{5}}{2}$$So, $D(\omega^2) > 0$ when $\omega^2 < \frac{k}{m}\frac{3-\sqrt{5}}{2}$ or $\omega^2 > \frac{k}{m}\frac{3+\sqrt{5}}{2}$.
The condition $r_2 > 0$, given that $D(\omega^2) > 0$, requires the numerator to be positive:
$$2k - m\omega^2 > 0 \implies \omega^2 < \frac{2k}{m}$$Combining all conditions: We need $\omega^2$ to satisfy both $D(\omega^2) > 0$ and $\omega^2 < 2k/m$. Since $\frac{3+\sqrt{5}}{2} \approx 2.618 > 2$, the condition $\omega^2 > \frac{k}{m}\frac{3+\sqrt{5}}{2}$ is incompatible with $\omega^2 < 2k/m$. Since $\frac{3-\sqrt{5}}{2} \approx 0.382 < 2$, the only valid range is the intersection of $\omega^2 < \frac{k}{m}\frac{3-\sqrt{5}}{2}$ and $\omega^2 < 2k/m$, which simplifies to the former.