Source: Physics Competition - Mechanics
Problem Sets:
Problem
As shown in the figure, three objects with masses $m_1$, $m_2$, and $m_3$ are hung in series and are initially at rest. Object 1 is attached above to an inextensible light string a. It is connected to object 2 by a light spring b, and object 2 is connected to object 3 by a light spring c. The springs are not necessarily identical.
- Find the acceleration of each object at the instant the string `a` is cut.
- Find the acceleration of the system's center of mass at that instant.
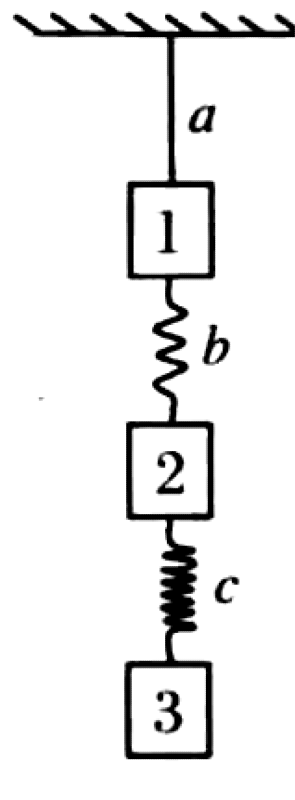
P0493-problem-1
The key principle is that at the instant a string is cut, its tension becomes zero, but the extension of a spring does not change instantaneously, so the spring force remains the same. Let the upward direction be positive.
Before cutting, the system is in equilibrium. The upward forces from the springs are:
$$F_c = m_3g$$ $$F_b = (m_2+m_3)g$$At the instant string a is cut, its tension becomes zero. The spring forces $F_b$ and $F_c$ are unchanged. We apply Newton's second law, $\sum F = ma$, to each mass.
For mass $m_1$: The forces are gravity $(-m_1g)$ and the downward pull from spring b $(-F_b)$.
$$-m_1g - F_b = m_1a_1$$ $$-m_1g - (m_2+m_3)g = m_1a_1$$ $$a_1 = -\frac{(m_1+m_2+m_3)g}{m_1}$$For mass $m_2$: The forces are the upward pull from spring b $(F_b)$, gravity $(-m_2g)$, and the downward pull from spring c $(-F_c)$.
$$F_b - m_2g - F_c = m_2a_2$$ $$(m_2+m_3)g - m_2g - m_3g = m_2a_2$$ $$0 = m_2a_2 \implies a_2 = 0$$For mass $m_3$: The forces are the upward pull from spring c $(F_c)$ and gravity $(-m_3g)$.
$$F_c - m_3g = m_3a_3$$ $$m_3g - m_3g = m_3a_3 \implies a_3 = 0$$For the center of mass (CM) of the system, after the cut, the only external force is gravity.
$$F_{ext} = -(m_1+m_2+m_3)g$$ $$M_{total} = m_1+m_2+m_3$$ $$a_{CM} = \frac{F_{ext}}{M_{total}} = \frac{-(m_1+m_2+m_3)g}{m_1+m_2+m_3} = -g$$The negative sign indicates downward acceleration for $a_1$ and $a_{CM}$.