Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in the figure, two fixed pulleys are separated by a distance $2d$. Two small balls A and B of equal mass are connected by a string that passes over the pulleys and supports a third ball C. As A and B descend with velocity $v$, ball C is pulled upward. At a certain moment, the angle between the two string segments connected to ball C is $2\alpha$. Neglect the mass of the string and pulleys, and any friction.
- Find the upward velocity of ball C at this moment.
- If balls A, B, and C all have mass $m$, and the system is released from rest when $\alpha=30^\circ$, what is the velocity of ball C when $\alpha'=45^\circ$?
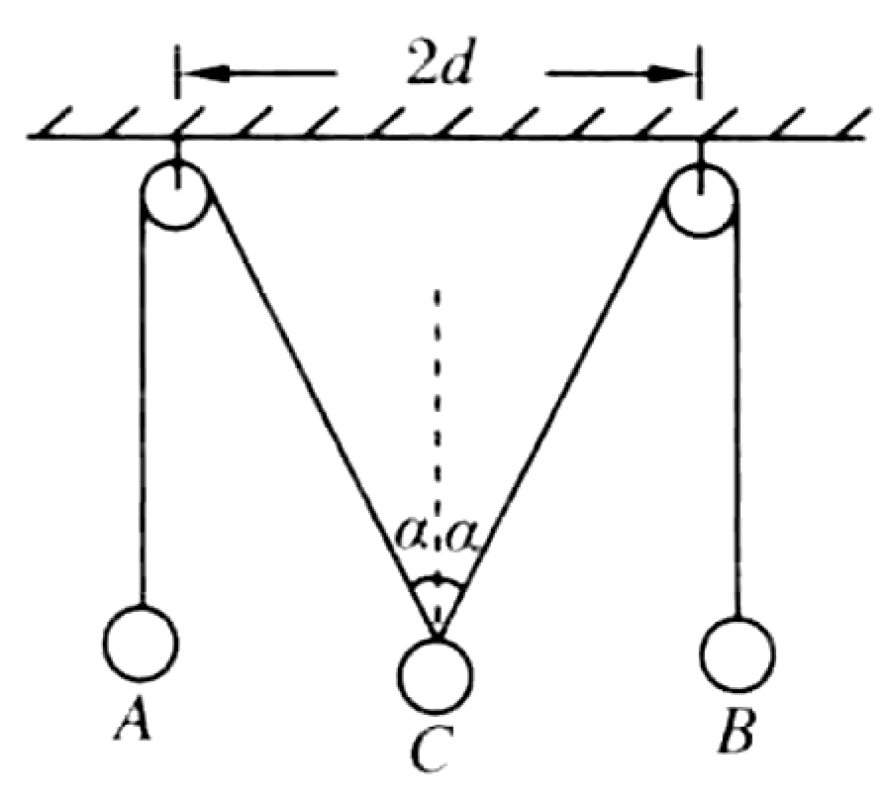
P0489-problem-1
[Q1] $v_C = v/\cos\alpha$ [Q2] $v_C = \sqrt{gd(5-2\sqrt{2}-\sqrt{3})}$
[Q1] The downward velocity $v$ of balls A and B is the speed of the string. The velocity of ball C, $v_C$, is vertical. The component of $v_C$ along the direction of the string must be equal to the string's speed. The angle between the vertical and the string is $\alpha$.
$$v = v_C \cos\alpha$$ $$v_C = \frac{v}{\cos\alpha}$$[Q2] We use the principle of conservation of mechanical energy for the system of three balls. Let the initial state be $\alpha_i = 30^\circ$ (at rest) and the final state be $\alpha_f = 45^\circ$. The vertical position of C below the pulleys is $y_C = d \cot\alpha$. The length of the string from a pulley to C is $l_s = d/\sin\alpha$. As C rises from $\alpha_i$ to $\alpha_f$, its height increases by $\Delta h_C = d(\cot\alpha_i - \cot\alpha_f)$. Balls A and B fall by a distance equal to the decrease in the slant length of the string, $\Delta h_{A,B} = d(1/\sin\alpha_i - 1/\sin\alpha_f)$. The total loss in potential energy is converted into kinetic energy.
$$PE_{loss} = 2mg\Delta h_{A,B} - mg\Delta h_C = mgd[2(\csc\alpha_i - \csc\alpha_f) - (\cot\alpha_i - \cot\alpha_f)]$$The final kinetic energy is $KE_{gain} = \frac{1}{2}mv_A^2 + \frac{1}{2}mv_B^2 + \frac{1}{2}mv_C^2$. From the velocity relation, $v_A = v_B = v_C \cos\alpha_f$.
$$KE_{gain} = 2\left(\frac{1}{2}m(v_C \cos\alpha_f)^2\right) + \frac{1}{2}mv_C^2 = \frac{1}{2}mv_C^2(2\cos^2\alpha_f + 1)$$Setting $PE_{loss} = KE_{gain}$:
$$mgd[2(2-\sqrt{2}) - (\sqrt{3}-1)] = \frac{1}{2}mv_C^2(2\cos^2 45^\circ + 1)$$ $$mgd(5-2\sqrt{2}-\sqrt{3}) = \frac{1}{2}mv_C^2(2(1/2)+1) = mv_C^2$$ $$v_C = \sqrt{gd(5-2\sqrt{2}-\sqrt{3})}$$