Source: High school physics (Chinese)
Problem Sets:
Problem
At point O, at a height $H=2$ m above the ground, a thin string of length $l=0.75$ m is fixed. A small ball of mass $m=0.1$ kg is attached to the end of the string. The maximum tension the string can withstand is $T_m = 15.0$ N. The string is held horizontally and the ball is given an initial vertically downward velocity $v_0 = 8$ m/s. When the string swings to the vertical position, it hits a nail at O' directly below O, where $OO' = l' = 0.5$ m.
- Will the string break?
- If the string breaks, where does the ball land? ($g=10$ m/s$^2$)
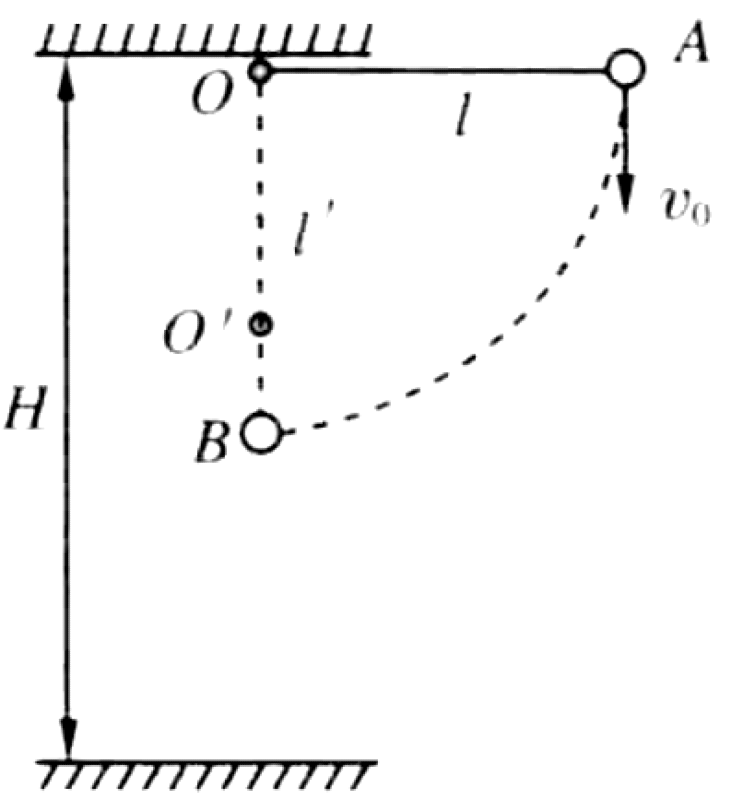
P0488-problem-1
[Q1] Yes, the string will break. [Q2] The ball lands at a horizontal distance of $x = 4.44$ m from the point directly below its release.
First, use conservation of mechanical energy to find the ball's speed, $v_B$, at the lowest point of its swing (B), just before the string hits the nail. Let the lowest point B be the zero potential energy level.
$$mgl + \frac{1}{2}mv_0^2 = \frac{1}{2}mv_B^2$$ $$v_B^2 = 2gl + v_0^2$$When the string hits the nail, the radius of the circular motion changes to $r = l - l'$. The speed of the ball remains $v_B$. The tension $T$ in the string is found by applying Newton's second law for circular motion:
$$T - mg = m \frac{v_B^2}{r}$$ $$T = mg + m \frac{2gl + v_0^2}{l-l'}$$Substitute values:
$T = (0.1)(10) + (0.1) \frac{2(10)(0.75) + 8^2}{0.75 - 0.5} = 1 + 0.1 \frac{15 + 64}{0.25} = 1 + 0.1 \frac{79}{0.25} = 32.6$ N.Since $T=32.6$ N $> T_m=15.0$ N, the string will break.
If the string breaks at point B, the ball becomes a projectile with an initial horizontal velocity $v_B$. The launch height above the ground is $h = H - l$. The time of flight $t$ is determined by the vertical motion:
$$h = \frac{1}{2}gt^2 \implies t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2(H-l)}{g}}$$The horizontal landing distance (range) $x$ is:
$$x = v_B t = \sqrt{2gl + v_0^2} \sqrt{\frac{2(H-l)}{g}}$$