Source: High school physics (Chinese)
Problem Sets:
Problem
A small ball of mass $m$ is attached to a light string of length $L$. The string's other end is fixed at a pivot point O. The ball is pulled to the side to a point A, where the string is horizontal, and then released from rest. It swings downward in a circular arc.
- What is the speed $v$ of the ball when it reaches the lowest point B of its trajectory?
- What is the tension $T$ in the string at this lowest point B?
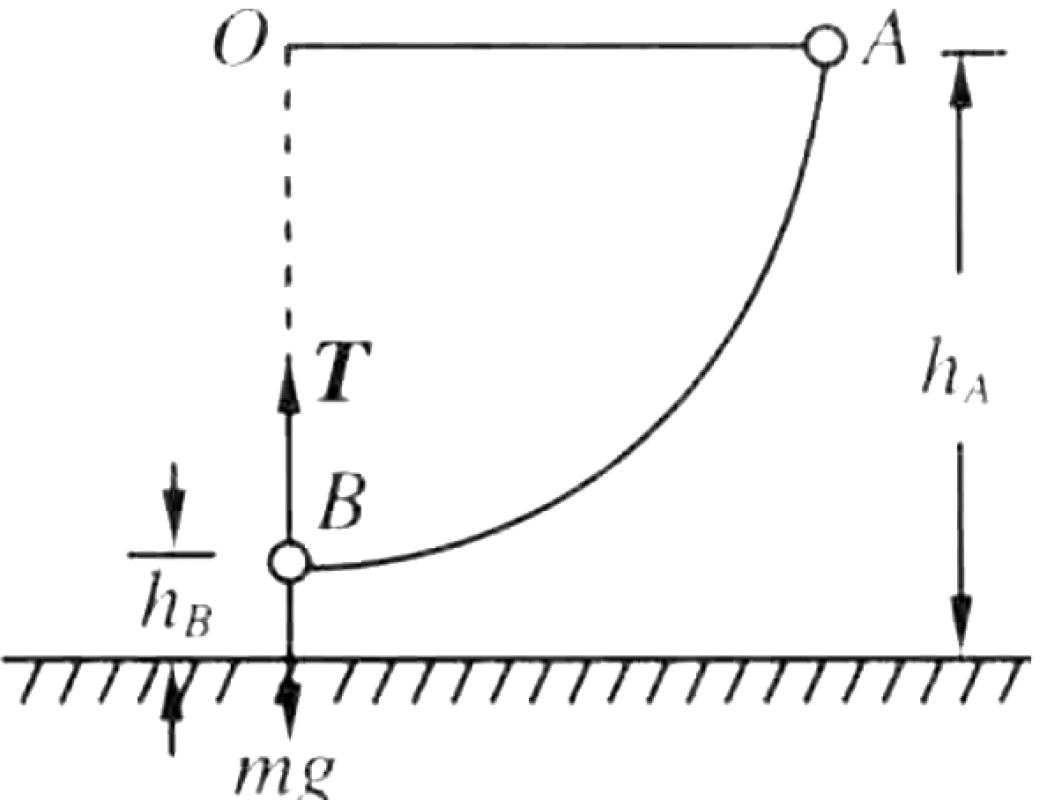
P0478-problem-1
[Q1] $v = \sqrt{2gL}$ [Q2] $T = 3mg$
Let the lowest point B be the reference level for gravitational potential energy ($U_B = 0$).
[Q1] We use the principle of conservation of mechanical energy. The initial state is at point A (string horizontal), and the final state is at the lowest point B. At point A, the height is $h_A = L$, and the speed is $v_A = 0$. The total energy is purely potential:
$$E_A = K_A + U_A = 0 + mgL = mgL$$At point B, the height is $h_B = 0$, and the speed is $v$. The total energy is purely kinetic:
$$E_B = K_B + U_B = \frac{1}{2}mv^2 + 0$$By conservation of energy, $E_A = E_B$:
$$mgL = \frac{1}{2}mv^2$$Solving for the speed $v$:
$$v^2 = 2gL \implies v = \sqrt{2gL}$$[Q2] At the lowest point B, the ball is undergoing circular motion. The net force towards the center of the circle (point O) provides the required centripetal force, $F_c = mv^2/L$. The forces acting on the ball are the upward tension $T$ and the downward gravitational force $mg$. Applying Newton's second law in the vertical direction:
$$\sum F_y = T - mg = \frac{mv^2}{L}$$Solving for the tension $T$:
$$T = mg + \frac{mv^2}{L}$$Substitute the expression for $v^2 = 2gL$ from the energy conservation step:
$$T = mg + \frac{m(2gL)}{L} = mg + 2mg = 3mg$$The tension at the bottom is three times the weight of the ball.