Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in the figure, a fixed pulley is installed on the edge of a smooth, fixed semicircular track of radius $R$. Two objects with masses $m_1$ and $m_2$ ($m_1 > m_2$) are connected by a light string passing over the pulley. The system is released from rest with $m_1$ at the top edge of the track, level with the pulley. It is known that $m_1$ can slide along the arc to the lowest point.
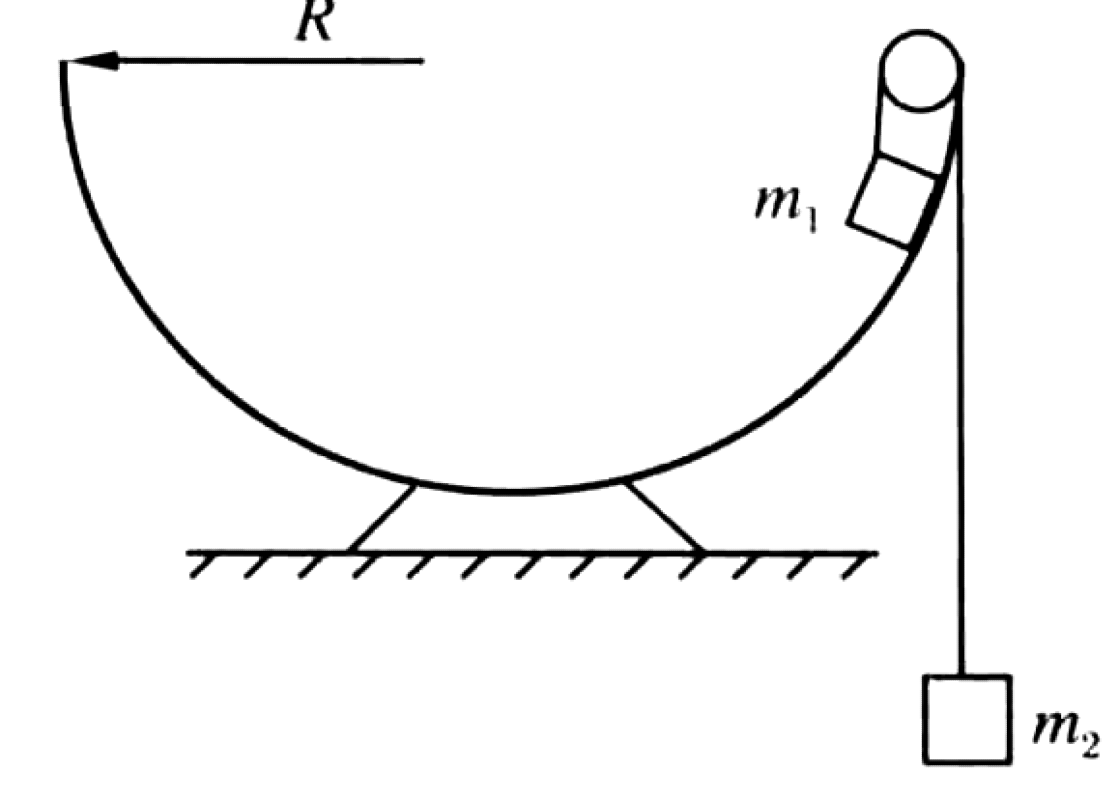
P0476-problem-1
We apply the principle of conservation of mechanical energy to the system of both masses and the Earth. Let the final speed of both masses be $v$.
The decrease in gravitational potential energy of $m_1$ as it moves down by a vertical distance $R$ is $\Delta PE_{1,loss} = m_1gR$.
As $m_1$ moves to the bottom of the track, the length of the string between the pulley and $m_1$ becomes the distance from a corner to the center of a square with side $R$, which is $\sqrt{R^2+R^2} = R\sqrt{2}$. This length of string is pulled over the pulley, so $m_2$ rises by a height of $R\sqrt{2}$. The increase in gravitational potential energy of $m_2$ is $\Delta PE_{2,gain} = m_2gR\sqrt{2}$.
The total gain in kinetic energy for the system is $\Delta KE = \frac{1}{2}m_1v^2 + \frac{1}{2}m_2v^2 = \frac{1}{2}(m_1+m_2)v^2$.
By conservation of energy, the net loss in potential energy equals the gain in kinetic energy:
$$ \Delta PE_{1,loss} - \Delta PE_{2,gain} = \Delta KE $$ $$ m_1gR - m_2gR\sqrt{2} = \frac{1}{2}(m_1+m_2)v^2 $$Solving for $v$:
$$ v^2 = \frac{2(m_1 - m_2\sqrt{2})gR}{m_1+m_2} $$