Source: High school physics (Chinese)
Problem Sets:
Problem
As shown in Figure below, a small block of mass m is released from rest at height H on a smooth track. The track becomes a vertical circular loop of radius R at the bottom. Neglect any resistance.
- What is the minimum height H required for the block to just pass through the highest point C of the circular loop?
- If the block is released from this minimum height H, what is the normal force it exerts on the track at the lowest point B?
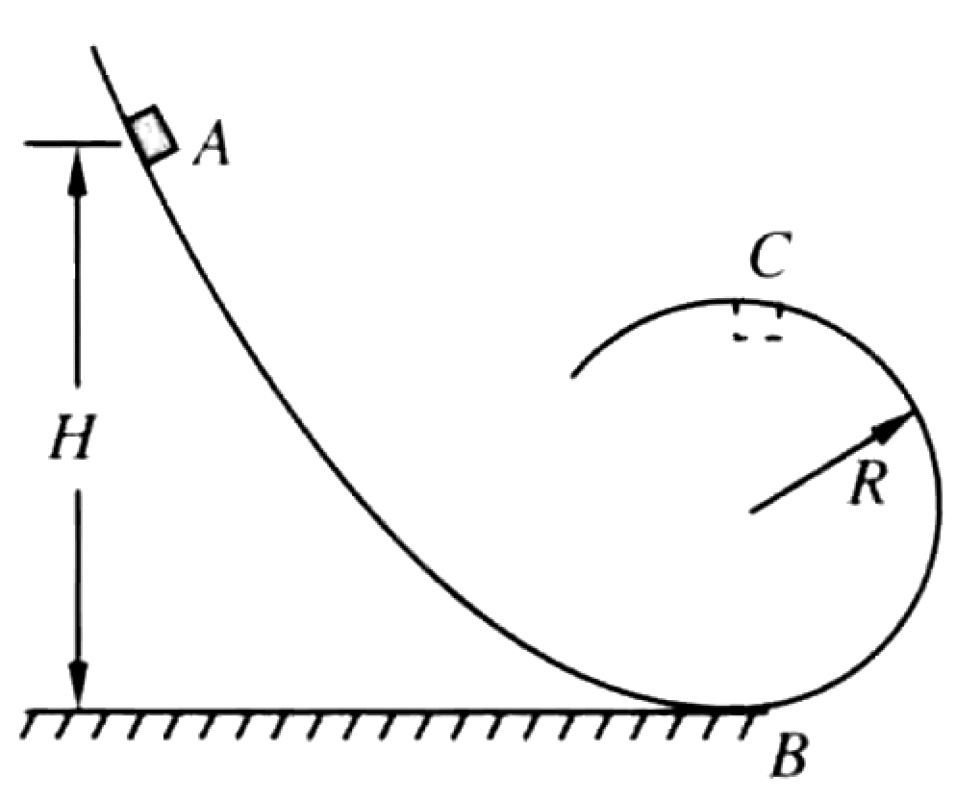
P0470-problem-1
[Q1] $H = \frac{5}{2}R$ [Q2] $F_{pressure} = 6mg$
[Q1] For the block to just pass the highest point C, the normal force from the track is zero. Gravity provides the required centripetal force. Let the speed at C be $v_C$.
$$mg = m\frac{v_C^2}{R} \implies v_C^2 = gR$$Apply the conservation of mechanical energy between the starting point (height H) and point C (height 2R).
$$E_{initial} = E_C$$ $$mgH = \frac{1}{2}mv_C^2 + mg(2R)$$Substitute $v_C^2 = gR$ into the energy equation:
$$mgH = \frac{1}{2}m(gR) + 2mgR$$ $$H = \frac{1}{2}R + 2R = \frac{5}{2}R$$[Q2] The block is released from $H = \frac{5}{2}R$. Apply conservation of energy between the start and the lowest point B (height 0). Let the speed at B be $v_B$.
$$E_{initial} = E_B$$ $$mgH = \frac{1}{2}mv_B^2$$ $$mg\left(\frac{5}{2}R\right) = \frac{1}{2}mv_B^2 \implies v_B^2 = 5gR$$At point B, the net force provides the centripetal force. The normal force $N_B$ points up and gravity $mg$ points down.
$$N_B - mg = m\frac{v_B^2}{R}$$ $$N_B = mg + m\frac{5gR}{R} = mg + 5mg = 6mg$$By Newton's third law, the pressure exerted by the block on the track equals $N_B$.