Source: Others
Problem Sets:
Problem
A pair of scissors are used to cut a wire of circular cross section and negligible weight. As the scissors clamps, the wire slides away from the hinge until the angle between the scissors blades becomes $2\alpha$. Find the friction coefficient $\mu$ between the blades and the wire. Assuming the static and kinetic friction is the same.
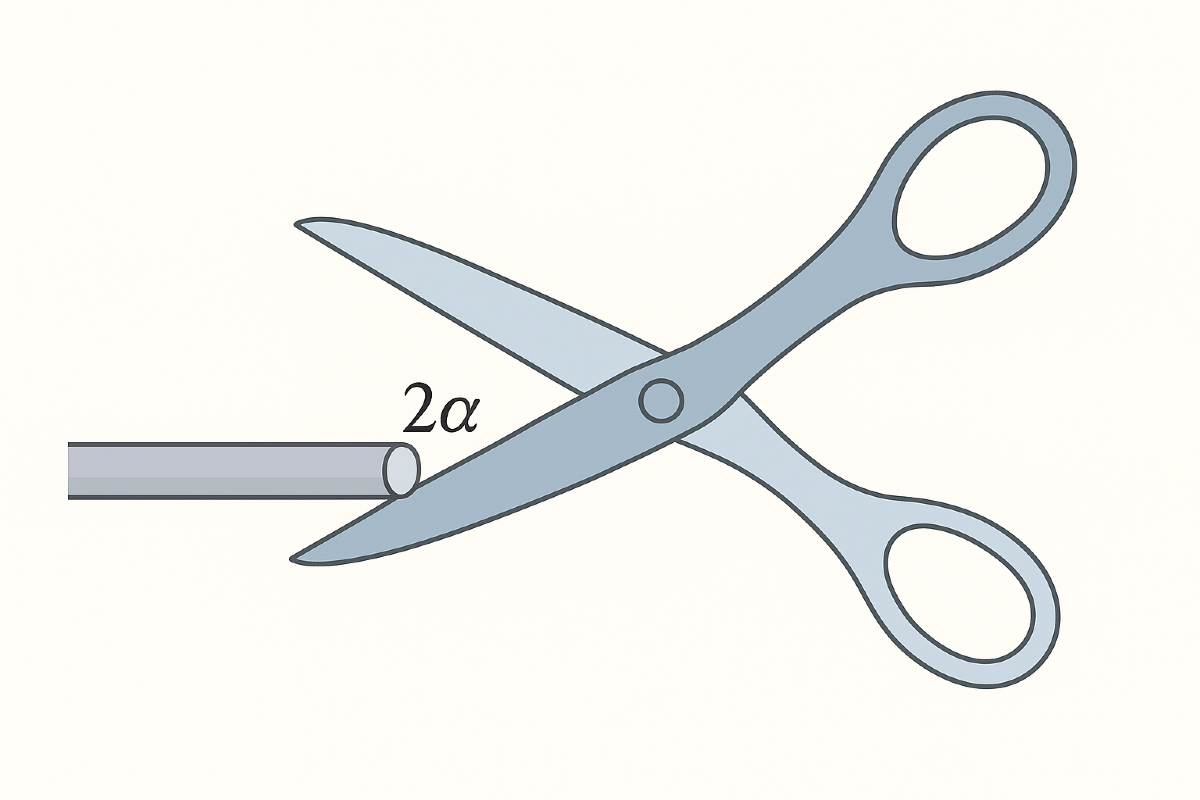
P0446-problem-1
Hints
Hint 1:
The friction coefficient $\mu$ between the blades and the wire is given by:
$$ \mu = \tan\alpha $$We analyze the forces acting on the wire at the moment it stops sliding. The wire is in a state of limiting static equilibrium. Let the axis of the wire be the x-axis, with the origin at the hinge of the scissors. The wire tends to slide in the +x direction (away from the hinge).
-
Free-Body Diagram and Forces: Consider a cross-section of the wire in the plane of the scissors. The two blades make an angle $2\alpha$ with each other. By symmetry, each blade makes an angle $\alpha$ with the wire's axis (the x-axis).
Each blade exerts two forces on the wire at the point of contact:
- A normal force $N$, perpendicular to the blade.
- A friction force $f$, parallel to the blade.
Since the wire tends to slide away from the hinge (in the +x direction), the friction force on each blade opposes this motion and points towards the hinge.
Let's resolve these forces into components parallel (x-direction) and perpendicular (y-direction) to the wire's axis.
-
For the top blade (at angle $+\alpha$ to the x-axis):
- The normal force $N$ points downwards and outwards. Its x-component is $N_x = N \sin\alpha$ and its y-component is $N_y = -N \cos\alpha$.
- The friction force $f$ points inwards. Its x-component is $f_x = -f \cos\alpha$ and its y-component is $f_y = -f \sin\alpha$.
-
For the bottom blade (at angle $-\alpha$ to the x-axis):
- By symmetry, the normal force has components $N_x = N \sin\alpha$ and $N_y = N \cos\alpha$.
- The friction force has components $f_x = -f \cos\alpha$ and $f_y = f \sin\alpha$.
-
Equilibrium Conditions: For the wire to be in equilibrium, the net force in all directions must be zero.
- Perpendicular to the wire (y-direction): The sum of the y-components is $\sum F_y = (-N\cos\alpha - f\sin\alpha) + (N\cos\alpha + f\sin\alpha) = 0$. This condition is satisfied by symmetry.
- Along the wire (x-direction): The outward push from the normal forces must be balanced by the inward pull from the friction forces.
-
Friction Law: The wire is on the verge of slipping, so the static friction force is at its maximum value:
$$ f = f_{s, \text{max}} = \mu N $$where $\mu$ is the coefficient of static friction.
-
Derivation of the Friction Coefficient: Substitute the expression for friction $f$ into the equilibrium equation for the x-direction:
$$ N \sin\alpha = (\mu N) \cos\alpha $$Since the blades are in contact with the wire, $N eq 0$, so we can divide both sides by $N$:
$$ \sin\alpha = \mu \cos\alpha $$Solving for the friction coefficient $\mu$:
$$ \mu = \frac{\sin\alpha}{\cos\alpha} = \tan\alpha $$
The result shows that the wire will slide out until the angle $\alpha$ becomes small enough that the friction can prevent further slipping, a condition determined solely by the coefficient of friction.