Source: High school physics (Chinese)
Problem
Two blocks of mass $m_1$ and $m_2$ are connected by a massless string and rest on a horizontal surface with a coefficient of kinetic friction $\mu_k$. A force $\vec{F}$ is applied to block $m_2$ at an angle $\theta$ below the horizontal, causing the system to accelerate.
- What is the tension $T$ in the string?
- What is the acceleration $a$ of the system?
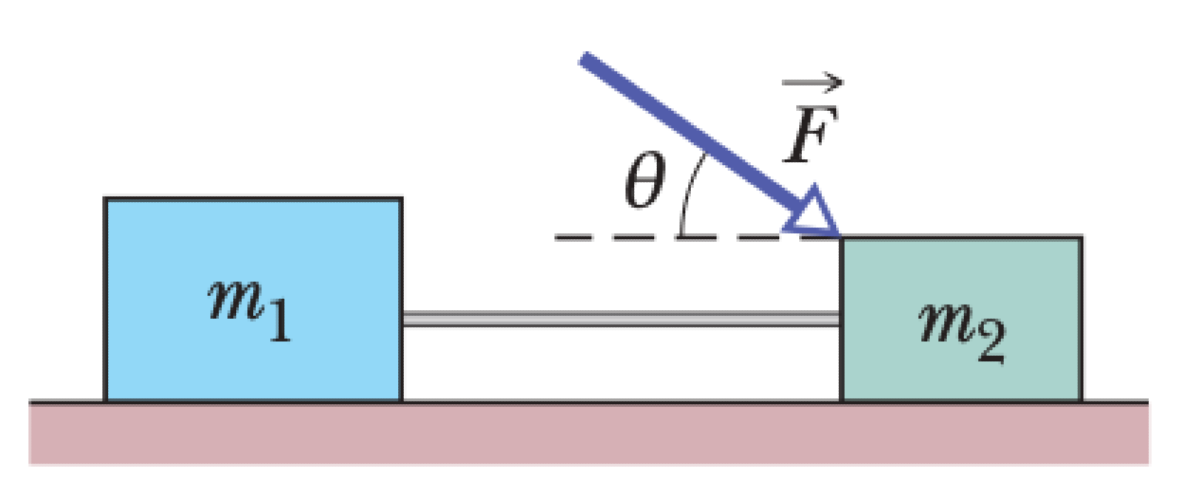
P0443-problem-1
[Q1] $T = \frac{m_1 F (\cos\theta - \mu_k \sin\theta)}{m_1+m_2}$ [Q2] $a = \frac{F (\cos\theta - \mu_k \sin\theta)}{m_1+m_2} - \mu_k g$
First, consider both blocks as a single system of mass $M = m_1 + m_2$. We apply Newton's second law in the vertical and horizontal directions.
In the vertical direction, the net force is zero. The normal force on block 1 is $N_1 = m_1 g$. For block 2, the downward component of $\vec{F}$ increases the normal force, so $N_2 = m_2 g + F \sin\theta$. The total normal force is $N_{total} = N_1 + N_2 = (m_1+m_2)g + F\sin\theta$.
The total kinetic friction force on the system is $f_{k,total} = \mu_k N_{total} = \mu_k ((m_1+m_2)g + F\sin\theta)$.
In the horizontal direction, the net force causes the system's acceleration $a$:
$$F \cos\theta - f_{k,total} = (m_1+m_2)a$$ $$a = \frac{F \cos\theta - \mu_k ((m_1+m_2)g + F\sin\theta)}{m_1+m_2}$$To find the tension $T$, we analyze the forces on block 1 alone. The tension pulls it to the right, and friction opposes the motion.
$$T - f_{k1} = m_1 a$$The friction on block 1 is $f_{k1} = \mu_k N_1 = \mu_k m_1 g$.
$$T = m_1 a + \mu_k m_1 g$$Substituting the expression for $a$:
$$T = m_1 \left( \frac{F \cos\theta - \mu_k ((m_1+m_2)g + F\sin\theta)}{m_1+m_2} \right) + \mu_k m_1 g$$ $$T = \frac{m_1 F \cos\theta - \mu_k m_1(m_1+m_2)g - \mu_k m_1 F\sin\theta + \mu_k m_1 g (m_1+m_2)}{m_1+m_2}$$The friction-gravity terms cancel, yielding the simplified expression for tension:
$$T = \frac{m_1 F (\cos\theta - \mu_k \sin\theta)}{m_1+m_2}$$