Source: High school physics (Chinese)
Problem Sets:
Problem
A crate of mass $m$ slides down an inclined trough. The trough is V-shaped with a right-angled cross-section and is inclined at an angle $\theta$ with respect to the horizontal. The coefficient of kinetic friction between the crate and the trough is $\mu_k$.
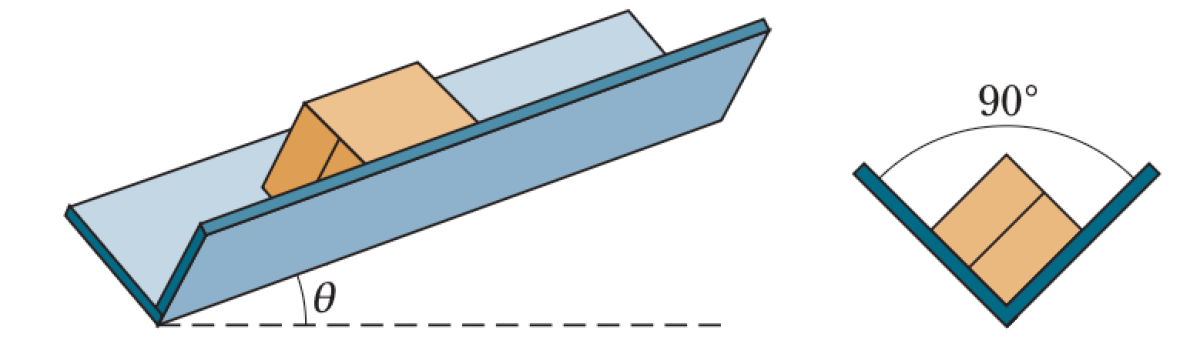
P0442-problem-1
Let the direction of motion down the incline be the x-axis. The net force in this direction determines the acceleration $a$.
$$ \sum F_x = mg\sin\theta - f_k = ma $$where $f_k$ is the total kinetic friction force.
The friction force is the sum of the friction from the two surfaces of the trough, $f_k = f_{k1} + f_{k2} = \mu_k N_1 + \mu_k N_2$. By symmetry, the normal forces from each surface are equal, $N_1 = N_2 = N$, so the total friction force is $f_k = 2\mu_k N$.
To find the normal force $N$, we analyze the forces in the plane perpendicular to the direction of motion. In this plane, the component of gravity is $mg\cos\theta$, which acts vertically downwards in the cross-sectional view. This force is balanced by the components of the two normal forces.
Since the trough has a 90° angle, each normal force vector makes an angle of 45° with the direction of the $mg\cos\theta$ component. Summing the forces in this direction:
$$ \sum F_\perp = N\cos(45^\circ) + N\cos(45^\circ) - mg\cos\theta = 0 $$ $$ 2N\cos(45^\circ) = mg\cos\theta $$Solving for N, with $\cos(45^\circ) = 1/\sqrt{2}$:
$$ 2N \left(\frac{1}{\sqrt{2}}\right) = mg\cos\theta \implies N = \frac{mg\cos\theta}{\sqrt{2}} $$Now, substitute $N$ into the expression for the total friction force:
$$ f_k = 2\mu_k \left(\frac{mg\cos\theta}{\sqrt{2}}\right) = \sqrt{2}\mu_k mg\cos\theta $$Finally, substitute the friction force back into Newton's second law for the x-direction:
$$ ma = mg\sin\theta - \sqrt{2}\mu_k mg\cos\theta $$Dividing by the mass $m$ gives the acceleration:
$$ a = g\sin\theta - \sqrt{2}\mu_k g\cos\theta = g(\sin\theta - \sqrt{2}\mu_k \cos\theta) $$