Source: High school physics (Chinese)
Problem Sets:
Problem
In Figure below, a 5.0 kg block is sent sliding up a plane inclined at $\theta = 37^\circ$ while a horizontal force $\vec{F}$ of magnitude 50 N acts on it. The coefficient of kinetic friction between block and plane is 0.30. The block's initial speed is 4.0 m/s.
- What are the (a) magnitude and (b) direction (up or down the plane) of the block's acceleration?
- How far up the plane does the block go?
- When it reaches its highest point, does it remain at rest or slide back down the plane?
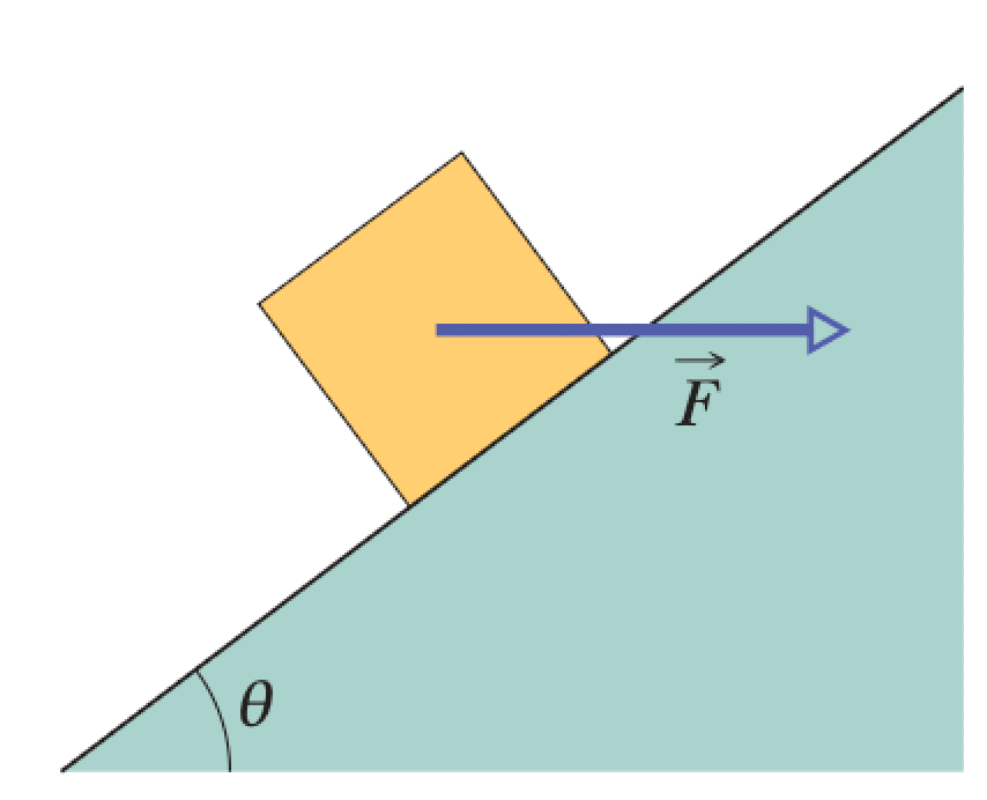
P0440-problem-1
[Q1] (a) $a = 2.1$ m/s$^2$, (b) down the plane [Q2] $d = 3.9$ m [Q3] It remains at rest.
Let the x-axis be parallel to the incline (positive up) and the y-axis be perpendicular to it. The forces on the block are gravity ($mg$), the normal force ($N$), the horizontal force ($F$), and kinetic friction ($f_k$).
(a), (b) While moving up, friction acts down the plane. Apply Newton's second law. In the y-direction: $\sum F_y = N - mg\cos\theta - F\sin\theta = 0$.
$$N = mg\cos\theta + F\sin\theta$$In the x-direction: $\sum F_x = F\cos\theta - mg\sin\theta - f_k = ma$. The kinetic friction is $f_k = \mu_k N = \mu_k(mg\cos\theta + F\sin\theta)$. Substituting for $f_k$ and solving for acceleration $a$:
$$a = \frac{F\cos\theta - mg\sin\theta - \mu_k(mg\cos\theta + F\sin\theta)}{m}$$ $$a = \frac{50\cos37^\circ - (5.0)(9.8)\sin37^\circ - 0.30((5.0)(9.8)\cos37^\circ + 50\sin37^\circ)}{5.0}$$ $$a = \frac{39.9\,\text{N} - 29.5\,\text{N} - 0.30(39.1\,\text{N} + 30.1\,\text{N})}{5.0\,\text{kg}} = \frac{10.4\,\text{N} - 20.8\,\text{N}}{5.0\,\text{kg}} = -2.08\,\text{m/s}^2$$The magnitude is $|a|$, and the negative sign indicates the direction is down the plane.
(c) The block stops when its final velocity $v_f$ is zero. Using kinematics:
$$v_f^2 = v_i^2 + 2ad$$ $$d = \frac{-v_i^2}{2a} = \frac{-(4.0\,\text{m/s})^2}{2(-2.08\,\text{m/s}^2)} = 3.85\,\text{m}$$(d) At the highest point, we check the condition for equilibrium. The tendency of motion is determined by comparing the parallel components of gravity and the applied force. Force component pushing up the plane: $F_{up} = F\cos\theta \approx 39.9$ N. Force component pulling down the plane: $F_{down} = mg\sin\theta \approx 29.5$ N. Since $F_{up} > F_{down}$, the block tends to move up the plane. Static friction, $f_s$, will oppose this by acting down the plane. For the block to remain at rest, the required static friction is:
$$f_s = F\cos\theta - mg\sin\theta = 39.9\,\text{N} - 29.5\,\text{N} = 10.4\,\text{N}$$The maximum available static friction is $f_{s,max} = \mu_s N$. Since $\mu_s \ge \mu_k$, the maximum friction is at least $f_k = \mu_k N = 20.8$ N. Because the required static friction ($10.4$ N) is less than the maximum available static friction ($\ge 20.8$ N), the block remains at rest.