Source: High school physics (Chinese)
Problem
A ball of mass $m = 1.34$ kg is connected by two massless strings, each of length $L = 1.70$ m, to a vertical, rotating rod. The strings are tied to the rod with a vertical separation $d = 1.70$ m and are taut. The ball rotates in a horizontal circle at a constant speed. The tension in the upper string is $T_u =35$ N.
- What is the tension $T_l$ in the lower string?
- What is the magnitude of the net force $\vec{F}_{net}$ on the ball?
- What is the speed $v$ of the ball?
- What is the direction of $\vec{F}_{net}$?
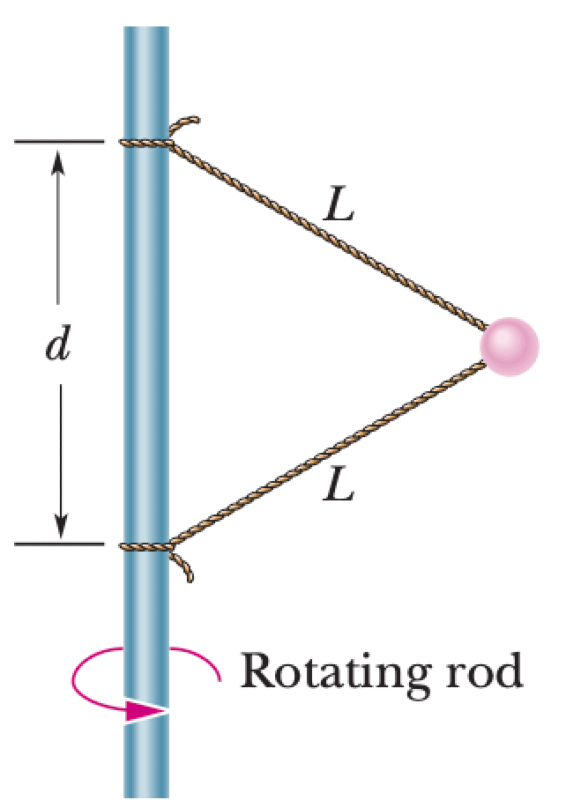
P0437-problem-1
[Q1] $T_l = T_u - \frac{2mgL}{d} = 8.74 \text{ N}$ [Q2] $F_{net} = \left(\frac{T_u}{L} - \frac{mg}{d}\right)\sqrt{4L^2-d^2} = 37.9 \text{ N}$ [Q3] $v = \sqrt{\frac{(4L^2-d^2)}{2m}\left(\frac{T_u}{L} - \frac{mg}{d}\right)} = 6.45 \text{ m/s}$ [Q4] Horizontally toward the rotating rod.
The geometry of the system defines the angle $\alpha$ each string makes with the vertical rod. The strings of length $L$ and the vertical separation $d$ form an isosceles triangle. We can find $\alpha$ using trigonometry:
$$\cos \alpha = \frac{d/2}{L} = \frac{d}{2L}$$The ball rotates in a horizontal circle of radius $r$:
$$r = L \sin \alpha$$Substituting the given values $d = 1.70$ m and $L = 1.70$ m:
$$\cos \alpha = \frac{1.70 \text{ m}}{2(1.70 \text{ m})} = 0.5 \implies \alpha = 60^\circ$$ $$r = (1.70 \text{ m}) \sin(60^\circ) = 1.70 \frac{\sqrt{3}}{2} \text{ m}$$We apply Newton's second law by analyzing the forces in the vertical and horizontal directions. The forces on the ball are the tension from the upper string ($T_u$), the tension from the lower string ($T_l$), and gravity ($mg$).
[Q1] What is the tension $T_l$ in the lower string? The ball has no vertical acceleration, so the net vertical force is zero.
$$\sum F_y = T_u \cos \alpha - T_l \cos \alpha - mg = 0$$Solving for $T_l$:
$$T_l = T_u - \frac{mg}{\cos \alpha}$$Substituting the given values:
$$T_l = 35 \text{ N} - \frac{(1.34 \text{ kg})(9.8 \text{ m/s}^2)}{0.5} = 35 \text{ N} - 26.264 \text{ N} = 8.736 \text{ N}$$ $$T_l = 8.74 \text{ N}$$[Q2] What is the magnitude of the net force $\vec{F}_{net}$ on the ball? The net force provides the centripetal acceleration, which is purely horizontal and directed towards the center of the circle.
$$\vec{F}_{net} = \sum \vec{F}_{horizontal}$$ $$F_{net} = T_u \sin \alpha + T_l \sin \alpha = (T_u + T_l)\sin \alpha$$Substituting the values for tensions and the angle:
$$F_{net} = (35 \text{ N} + 8.736 \text{ N}) \sin(60^\circ) = (43.736 \text{ N}) \frac{\sqrt{3}}{2}$$ $$F_{net} = 37.9 \text{ N}$$[Q3] What is the speed $v$ of the ball? The net force is the centripetal force, $F_c = mv^2/r$.
$$F_{net} = \frac{mv^2}{r}$$Solving for the speed $v$:
$$v = \sqrt{\frac{F_{net}r}{m}}$$Substituting the values for $F_{net}$, $r$, and $m$:
$$v = \sqrt{\frac{(37.876 \text{ N})(1.70 \frac{\sqrt{3}}{2} \text{ m})}{1.34 \text{ kg}}} = \sqrt{\frac{55.76 \text{ N} \cdot \text{m}}{1.34 \text{ kg}}}$$ $$v = 6.45 \text{ m/s}$$[Q4] What is the direction of $\vec{F}_{net}$? For an object in uniform circular motion, the net force is the centripetal force, which always points towards the center of the circular path. In this case, the path is a horizontal circle. The direction of $\vec{F}_{net}$ is horizontal, pointing towards the central rotating rod.