Source: High school physics (Chinese)
Problem
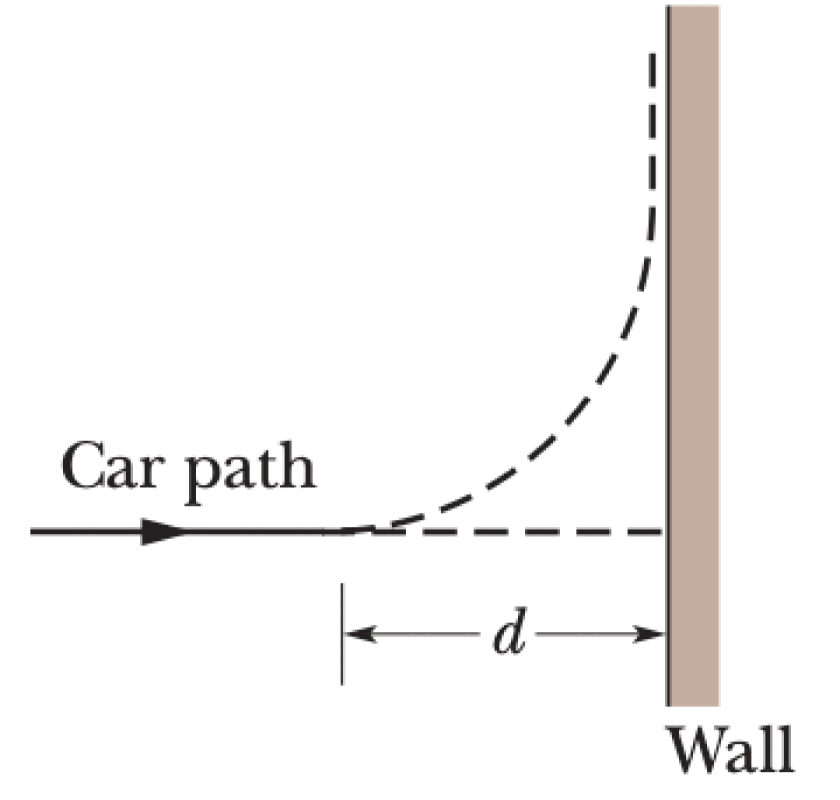
Figure depicts an overhead view of a car's path as it travels toward a wall. Assume that the driver begins to brake the car when the distance to the wall is $d$, and take the car's mass as $m$, its initial speed as $v_0$, the coefficient of static friction as $\mu_s$, and the coefficient of kinetic friction as $\mu_k$. Assume that the car's weight is distributed evenly on the four wheels.
- What magnitude of static friction $f_s$ is needed (between tires and road) to stop the car just as it reaches the wall?
- What is the maximum possible static friction $f_{s,max}$?
- If the coefficient of kinetic friction between the (sliding) tires and the road is $\mu_k$, at what speed $v_f$ will the car hit the wall?
- To avoid the crash, a driver could elect to turn the car so that it just barely misses the wall, as shown in the figure. What magnitude of frictional force $f_c$ would be required to keep the car in a circular path of radius $d$ and at the given speed $v_0$?
- Is the required force for turning less than the maximum possible static friction, so that a circular path is possible?
P0436-problem-1
[Q1] $f_s = \frac{m v_0^2}{2d}$ [Q2] $f_{s,max} = \mu_s mg$ [Q3] $v_f = \sqrt{v_0^2 - 2\mu_k g d}$ [Q4] $f_c = \frac{m v_0^2}{d}$ [Q5] The turn is possible if $\frac{v_0^2}{gd} \le \mu_s$.
The normal force on the car is $N = mg$.
[Q1] To stop the car over a distance $d$, we use the kinematic equation $v^2 = v_0^2 + 2ad$. With final velocity $v=0$, the acceleration required is $a = -v_0^2 / (2d)$. The force needed is the static friction $f_s$ (for non-skidding brakes).
$$f_s = |ma| = m \frac{v_0^2}{2d}$$[Q2] The maximum static friction is defined by the coefficient of static friction $\mu_s$ and the normal force $N$.
$$f_{s,max} = \mu_s N = \mu_s mg$$[Q3] If the car skids, the braking force is the kinetic friction, $f_k = \mu_k N = \mu_k mg$. The acceleration is $a = -f_k / m = -\mu_k g$. Using the same kinematic equation:
$$v_f^2 = v_0^2 + 2ad = v_0^2 - 2\mu_k g d$$ $$v_f = \sqrt{v_0^2 - 2\mu_k g d}$$This assumes the car does not stop before hitting the wall ($v_0^2 > 2\mu_k g d$).
[Q4] For the car to turn in a circular path of radius $r=d$ at a constant speed $v_0$, the static friction must provide the necessary centripetal force $f_c$.
$$f_c = m a_c = m \frac{v_0^2}{r} = m \frac{v_0^2}{d}$$[Q5] The turn is possible if the required centripetal force $f_c$ is less than or equal to the maximum available static friction $f_{s,max}$.
$$f_c \le f_{s,max}$$ $$m \frac{v_0^2}{d} \le \mu_s mg$$The condition for the turn to be possible is:
$$\frac{v_0^2}{gd} \le \mu_s$$