Dynamics
Beginner
Circular Motion
Source: High school physics (Chinese)
Problem
A puck of mass $m$ slides in a circle of radius $r$ on a frictionless table. The puck is attached to a hanging cylinder of mass $M$ by a cord that extends through a hole in the table.
What speed $v$ must the puck have for the cylinder to remain at rest? Express your answer in terms of $m$, $M$, $g$, and $r$.
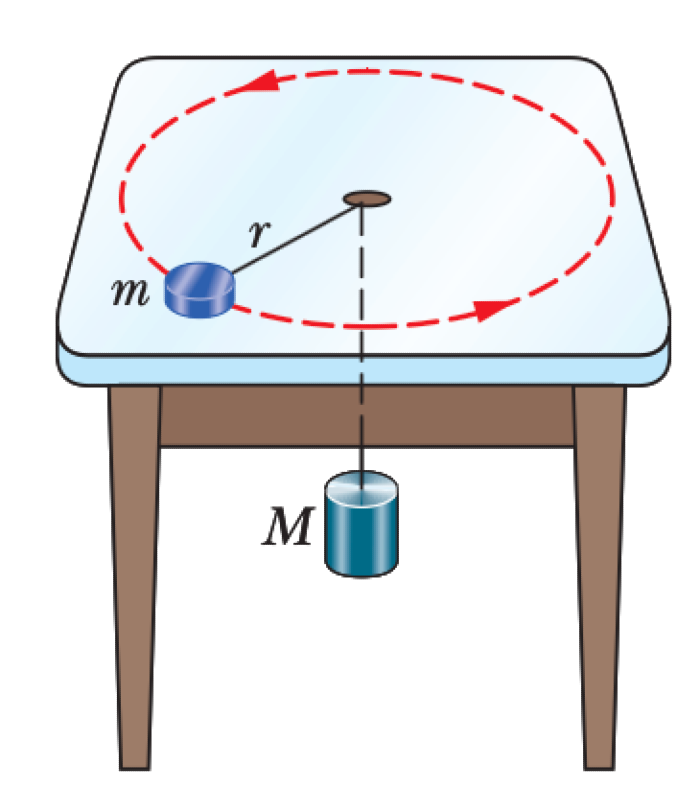
P0435-problem-1
$v = \sqrt{\frac{Mgr}{m}}$
For the hanging cylinder of mass $M$ to remain at rest, the net force on it must be zero. The upward tension $T$ in the cord must balance the downward gravitational force $F_g = Mg$.
$$T = Mg$$For the puck of mass $m$ to move in a uniform circle, the net force on it must provide the centripetal force, $F_c = mv^2/r$. This force is supplied by the tension $T$ in the cord.
$$T = \frac{mv^2}{r}$$Equating the two expressions for tension and solving for the speed $v$:
$$Mg = \frac{mv^2}{r}$$ $$v^2 = \frac{Mgr}{m}$$ $$v = \sqrt{\frac{Mgr}{m}}$$