Source: High school physics (Chinese)
Problem
A bolt is threaded onto one end of a thin horizontal rod, and the rod is then rotated horizontally about its other end. An engineer monitors the motion by flashing a strobe lamp onto the rod and bolt, adjusting the strobe rate until the bolt appears to be in the same eight places during each full rotation ofthe rod. The strobe rate is 2000 flashes per second; the bolt has mass 30 g and is at radius 3.5 cm.
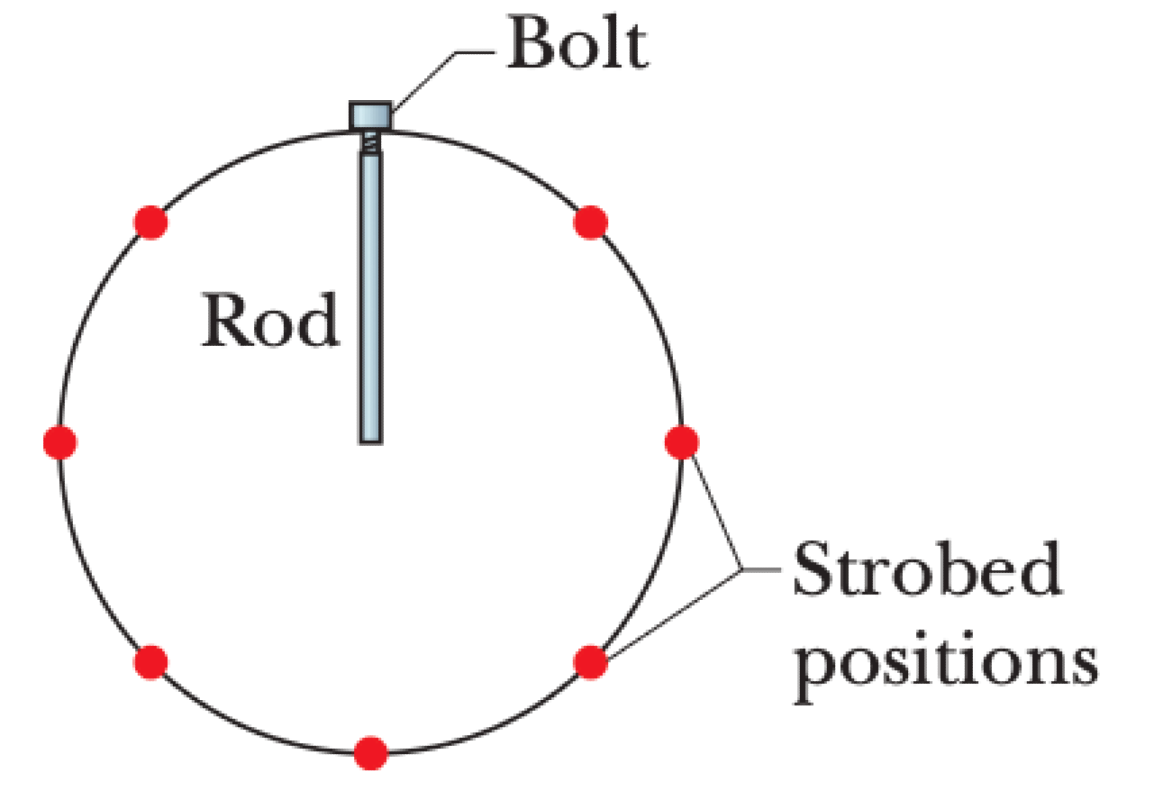
P0433-problem-1
The force on the bolt from the rod is the centripetal force, $F_c$, required to maintain the bolt's circular motion. The magnitude of this force is given by Newton's second law:
$$F_c = ma_c = m\omega^2 r$$where $m$ is the mass of the bolt, $\omega$ is its angular velocity, and $r$ is the radius of its circular path.
The angular velocity $\omega$ can be determined from the stroboscopic observation. The strobe lamp flashes at a frequency $f_{strobe} = 2000 \text{ Hz}$. The time between flashes is $T_{strobe} = 1/f_{strobe}$. Since the bolt appears in $N=8$ distinct, equally spaced positions during one full rotation, the time for the rod to complete $1/N$ of a revolution must be equal to the time between flashes. The period of rotation, $T$, is therefore:
$$T = N T_{strobe} = \frac{N}{f_{strobe}}$$The angular velocity is related to the period by $\omega = 2\pi/T$. Substituting the expression for $T$:
$$\omega = \frac{2\pi}{N/f_{strobe}} = \frac{2\pi f_{strobe}}{N}$$Now, substitute this expression for $\omega$ into the centripetal force equation:
$$F_c = m \left( \frac{2\pi f_{strobe}}{N} \right)^2 r$$Substituting the given values:
$m = 30 \text{ g} = 0.030 \text{ kg}$ $r = 3.5 \text{ cm} = 0.035 \text{ m}$ $f_{strobe} = 2000 \text{ s}^{-1}$ $N = 8$ $$F_c = (0.030 \text{ kg}) \left( \frac{2\pi (2000 \text{ s}^{-1})}{8} \right)^2 (0.035 \text{ m})$$ $$F_c = (0.030 \text{ kg}) (500\pi \text{ s}^{-1})^2 (0.035 \text{ m})$$ $$F_c = 262.5 \pi^2 \text{ N} \approx 2590.8 \text{ N}$$Rounding to two significant figures, consistent with the given data:
$$F_c \approx 2600 \text{ N}$$