Source: High school physics (Chinese)
Problem
A passenger of mass $m$ is in uniform circular motion along a path of radius $r$. The magnitude of the net centripetal force is $F$.
- A plot of $F$ versus the passenger's speed $v$ is generated as in Figure a. What is the plot's slope at a given speed $v$?
- A plot of $F$ versus the period of motion $T$ is generated as in Figure b. What is the plot's slope at a given period $T$?
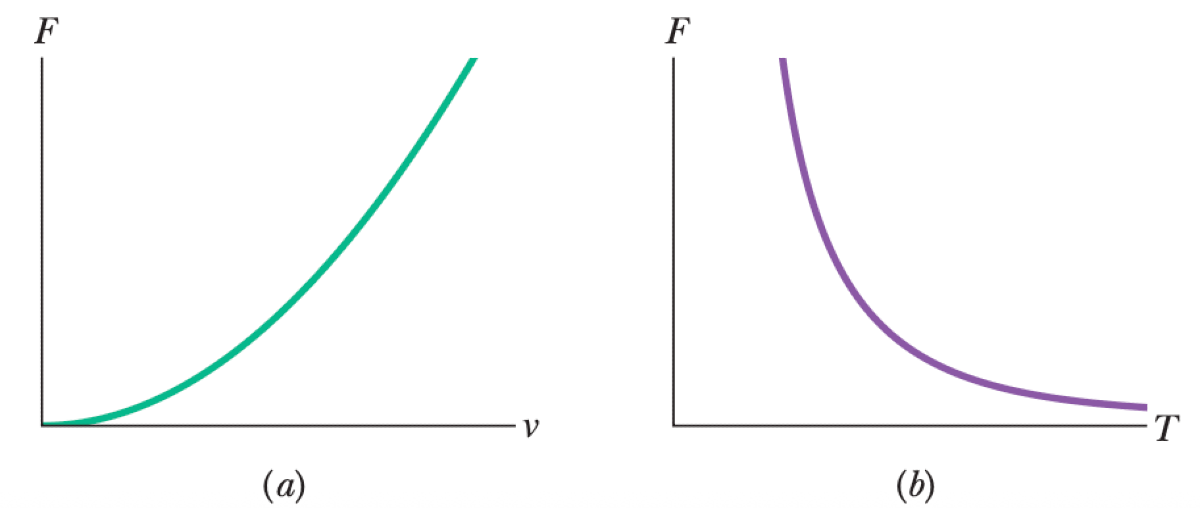
P0431-problem-1
[Q1] $S_v = \frac{2mv}{r}$ [Q2] $S_T = -\frac{8\pi^2 mr}{T^3}$
The centripetal force $F$ is given by Newton's second law for circular motion:
$$F = ma_c = \frac{mv^2}{r}$$[Q1] The slope of the $F$ versus $v$ plot, $S_v$, is the derivative of $F$ with respect to $v$.
$$S_v = \frac{dF}{dv} = \frac{d}{dv}\left(\frac{mv^2}{r}\right)$$Applying the power rule for differentiation:
$$S_v = \frac{m}{r}(2v) = \frac{2mv}{r}$$[Q2] To find the slope of the $F$ versus $T$ plot, we first express $F$ as a function of $T$. The speed $v$ is related to the period $T$ and radius $r$ by $v = 2\pi r / T$. Substituting this into the force equation:
$$F = \frac{m}{r}\left(\frac{2\pi r}{T}\right)^2 = \frac{m}{r}\frac{4\pi^2 r^2}{T^2} = \frac{4\pi^2 mr}{T^2}$$The slope of the $F$ versus $T$ plot, $S_T$, is the derivative of $F$ with respect to $T$.
$$S_T = \frac{dF}{dT} = \frac{d}{dT}\left(4\pi^2 mr T^{-2}\right)$$Applying the power rule:
$$S_T = 4\pi^2 mr (-2T^{-3}) = -\frac{8\pi^2 mr}{T^3}$$