Source: High school physics (Chinese)
Problem
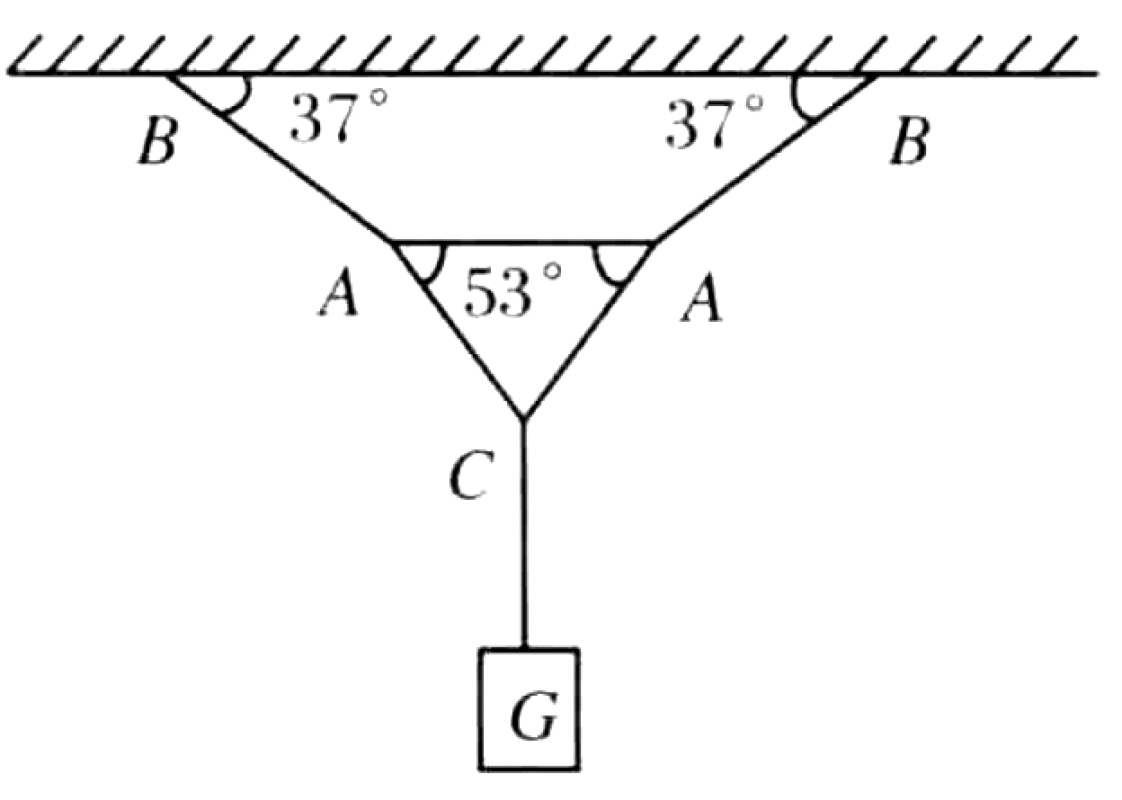
An object of weight $W$ is held in static equilibrium by a symmetric system of ropes as shown. A central point C is supported by two ropes AC, each making an angle $\beta$ with the vertical. Each connection point A is in turn supported by a rope AB attached to a horizontal ceiling, with each rope AB making an angle $\alpha$ with the horizontal. Let the tensions in the ropes be $T_{CG}$, $T_{AC}$, and $T_{AB}$. The system is in static equilibrium.
- Find the tension $T_{CG}$ in the rope supporting the weight.
- Find the tension $T_{AC}$ in the ropes AC.
- Find the tension $T_{AB}$ in the ropes AB. Simplify the result for the special case where the angles are complementary, i.e., $\alpha + \beta = \pi/2$.
01K5Z1QC5SKQQS9KAQV0AP2CFH
01K5Z1QC5SKQQS9KAQV0AP2CFH
[Q1] $T_{CG} = W$ [Q2] $T_{AC} = \frac{W}{2\cos\beta}$ [Q3] $T_{AB} = \frac{W}{2\sin\alpha}$. In the special case where $\alpha + \beta = \pi/2$, this becomes $T_{AB} = T_{AC} = \frac{W}{2\cos\beta}$.
We apply the condition for static equilibrium ($\sum \vec{F} = 0$) to the connection points (knots) C and A. By symmetry, the tensions in the two AC ropes are equal, as are the tensions in the two AB ropes.
-
Analysis of Knot C: The tension in the lowest rope directly supports the weight.
$$T_{CG} = W$$The vertical components of the two tensions $T_{AC}$ must balance the weight $W$.
$$\sum F_y = 2 T_{AC} \cos\beta - W = 0$$ $$T_{AC} = \frac{W}{2\cos\beta}$$The horizontal components of the $T_{AC}$ tensions cancel due to symmetry.
-
Analysis of Knot A: For knot A to be in equilibrium under the action of only two forces ($T_{AC}$ and $T_{AB}$), the net force must be zero. We analyze the force components. Vertical equilibrium:
$$\sum F_y = T_{AB} \sin\alpha - T_{AC} \cos\beta = 0 \implies T_{AB} = T_{AC} \frac{\cos\beta}{\sin\alpha}$$Substituting the expression for $T_{AC}$:
$$T_{AB} = \left(\frac{W}{2\cos\beta}\right) \frac{\cos\beta}{\sin\alpha} = \frac{W}{2\sin\alpha}$$Horizontal equilibrium requires $T_{AB}\cos\alpha - T_{AC}\sin\beta = 0$. This condition is only met if the angles are complementary ($\alpha + \beta = \pi/2$), which makes $\sin\beta = \cos\alpha$ and $\cos\beta = \sin\alpha$. This specific geometry ensures that knot A is in equilibrium without any additional forces.
For the special case $\alpha + \beta = \pi/2$, we use $\sin\alpha = \cos\beta$. The vertical equilibrium equation at knot A simplifies:
$$T_{AB} \sin\alpha - T_{AC} \sin\alpha = 0 \implies T_{AB} = T_{AC}$$Therefore, the tension $T_{AB}$ is the same as $T_{AC}$.