Source: Principles of Physics
Problem
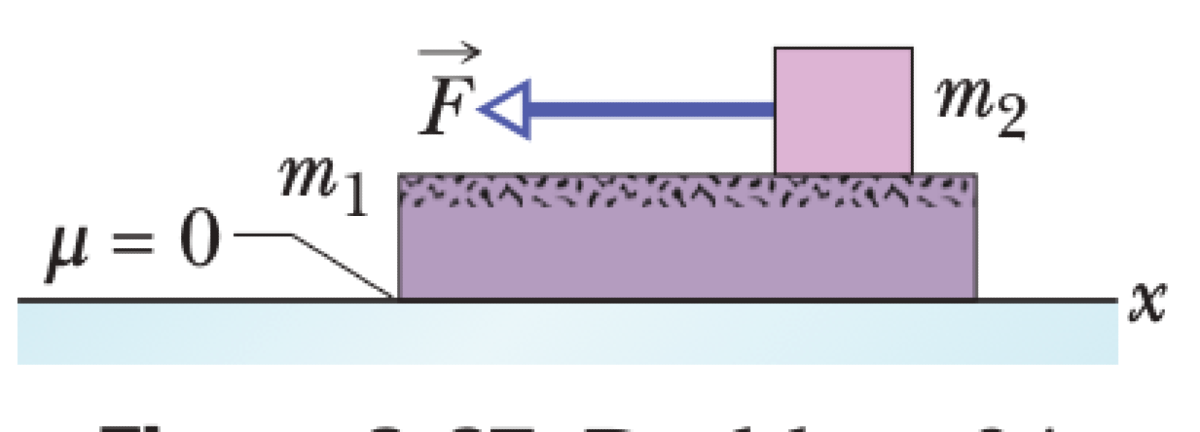
A slab of mass $m_1$ rests on a frictionless floor. A block of mass $m_2$ rests on the slab. The coefficients of static and kinetic friction between the block and slab are $\mu_s$ and $\mu_k$, respectively. A horizontal force of magnitude $F$ is applied to the block in the positive x-direction.
- Find the acceleration of the block, $\vec{a}_2$.
- Find the acceleration of the slab, $\vec{a}_1$.
01K63JYE31CTSGM696A72MH2K4
[Q1] $\vec{a}_2 = \left( \frac{F}{m_2} - \mu_k g \right) \hat{i}$ [Q2] $\vec{a}_1 = \left( \frac{\mu_k m_2 g}{m_1} \right) \hat{i}$
First, we determine if the block slips on the slab. If they move together, the system's acceleration would be $a_{sys} = \frac{F}{m_1 + m_2}$. The force required to accelerate the slab at this rate is provided by static friction, $f_{s,req} = m_1 a_{sys} = \frac{m_1 F}{m_1 + m_2}$.
The maximum available static friction force is $f_{s,max} = \mu_s N_2 = \mu_s m_2 g$. Slipping occurs if the required force exceeds the maximum available force, i.e., if $f_{s,req} > f_{s,max}$. This condition implies that the bodies move separately.
When the block slips, a kinetic friction force $f_k = \mu_k m_2 g$ acts. We apply Newton's second law to each body individually.
For the block ($m_2$), the net force is the applied force minus the opposing kinetic friction:
$$F - f_k = m_2 a_2 \implies a_2 = \frac{F - \mu_k m_2 g}{m_2}$$For the slab ($m_1$), the only horizontal force is the kinetic friction exerted by the block, which acts in the direction of motion:
$$f_k = m_1 a_1 \implies a_1 = \frac{\mu_k m_2 g}{m_1}$$