Source: Principles of Physics
Problem
Block A of weight $W_A$ rests on a horizontal table. It is connected by a string passing over a frictionless, massless pulley to a hanging block B of weight $W_B$. A third block C, of weight $W_C$, is placed on top of block A. The coefficient of static friction between block A and the table is $\mu_s$, and the coefficient of kinetic friction is $\mu_k$.
- Determine the minimum weight of block C ($W_C$) required to keep the system from sliding.
- If block C is suddenly removed, what is the acceleration ($a$) of block A? (Assume $W_B > \mu_s W_A$).
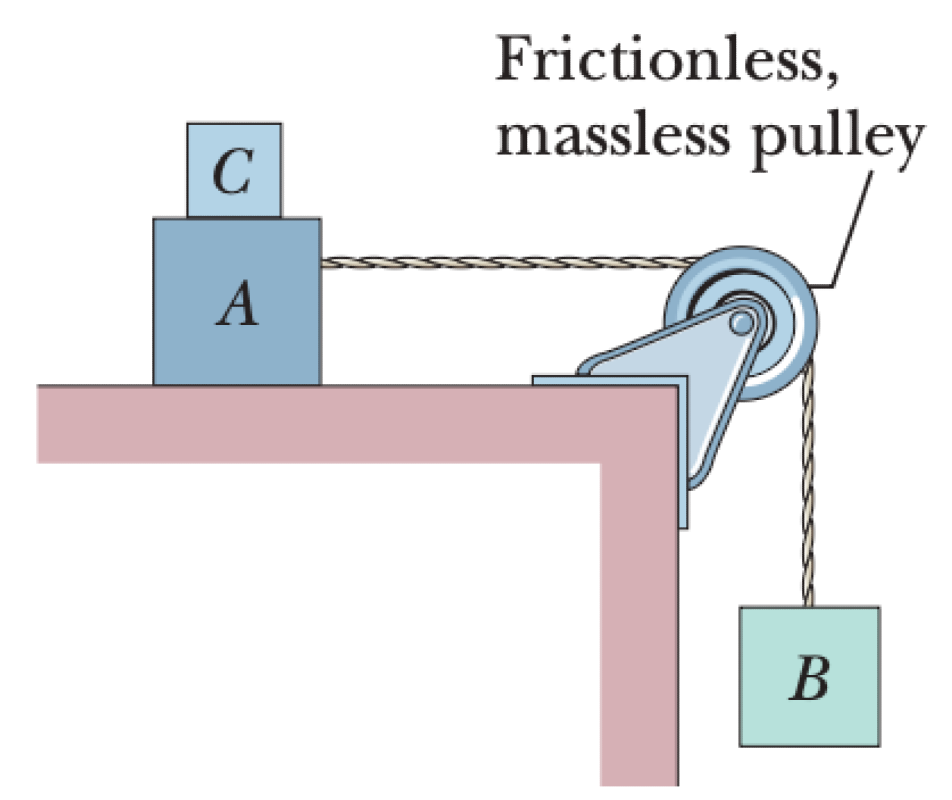
01K63JTVPR7KEEF1D3PT738GCE
[Q1] $W_C = \frac{W_B}{\mu_s} - W_A$ [Q2] $a = g \frac{W_B - \mu_k W_A}{W_A + W_B}$
For Q1, the system is in static equilibrium. The tension $T$ from block B's weight is balanced by the maximum static friction force $f_{s,max}$ on the combined blocks A and C.
$$T = W_B$$The normal force is $N = W_A + W_C$, so the friction force is:
$$f_{s,max} = \mu_s N = \mu_s (W_A + W_C)$$For equilibrium, $T = f_{s,max}$, which gives:
$$W_B = \mu_s (W_A + W_C)$$Solving for $W_C$ yields the minimum weight required.
For Q2, block C is removed. The system (blocks A and B) accelerates. The net force on the system is the weight of B minus the kinetic friction force $f_k$ on A. The total mass is $M = m_A + m_B = (W_A + W_B)/g$. Applying Newton's second law, $F_{net} = Ma$:
$$W_B - f_k = \left(\frac{W_A + W_B}{g}\right)a$$The kinetic friction is $f_k = \mu_k N' = \mu_k W_A$. Substituting this in:
$$W_B - \mu_k W_A = \left(\frac{W_A + W_B}{g}\right)a$$Solving for acceleration $a$ gives the final expression.