Source: Principles of Physics
Problem
Two blocks are connected over a frictionless, massless pulley as shown in the figure. The mass of block A is $m_A$. The coefficient of kinetic friction between block A and the incline is $\mu_k$. The angle of the incline is $\theta$. Block A slides down the incline at a constant speed. The connecting rope has negligible mass.
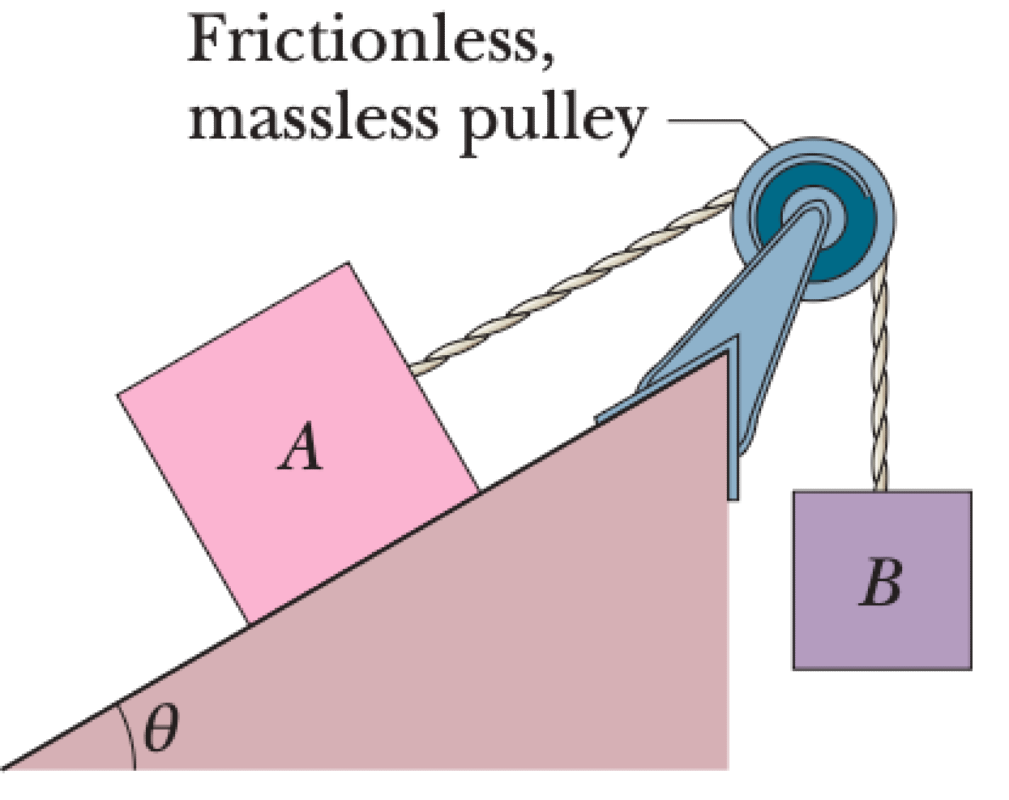
01K63K0RXQXRJ60D3GGSY4QRAQ
Since the system moves at a constant velocity, the net acceleration is zero ($a=0$). We apply Newton's second law to each block. Let $T$ be the tension in the rope.
For the hanging block B, the forces are balanced:
$$T - m_B g = 0 \implies T = m_B g$$For block A, we analyze forces along the incline. The component of gravity pulling the block down the incline is $m_A g \sin\theta$. Since the block moves down the incline, tension $T$ and the kinetic friction force $f_k$ both act up the incline, opposing the motion. The force balance equation is:
$$m_A g \sin\theta - T - f_k = 0$$The kinetic friction force is $f_k = \mu_k N$, where the normal force $N$ is equal to the perpendicular component of block A's weight, $N = m_A g \cos\theta$. Thus, $f_k = \mu_k m_A g \cos\theta$.
Substituting the expressions for $T$ and $f_k$ into the force balance equation for block A:
$$m_A g \sin\theta - m_B g - \mu_k m_A g \cos\theta = 0$$Solving for $m_B$ by dividing by $g$ and rearranging:
$$m_B = m_A \sin\theta - \mu_k m_A \cos\theta$$